Question

(a) Show with the help of a diagram, how unpolarised sunlight gets polarised due to scattering.
(b) Two polaroids ${P_1}$ and ${P_2}$ are placed with their pass axes perpendicular to each other. Unpolarised light of intensity ${I_0}$ is incident on ${P_1}$. A third polaroid ${P_3}$ is kept in between ${P_1}$ and ${P_2}$ such that its pass axis makes an angle of ${45^0}$ with that of ${P_1}$. Determine the intensity of light transmitted through ${P_1},$ ${P_2},$ and ${P_3}$.

Answer 1

Hint: Light, that has electric and magnetic vector components vibrating along the direction perpendicular to the direction of the light and also perpendicular to each other is called unpolarised light. The process of confining the direction of vibration of electric and magnetic vectors of light is called polarization. The intensity of light after polarization is given by Malus law.

Complete step by step answer:
Every transverse wave has electric and magnetic vectors vibrating along the direction perpendicular to the direction of the wave and also perpendicular to each other.
Observe the diagram

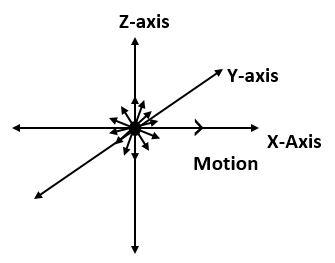
In the above diagram, motion represents the direction of motion of light along XZ-plane. The small arrows represent the direction of vibration of electric vectors along the YZ-plane. And the big dot in the middle represents the direction of vibration of the magnetic vector along XY-plane.
Such a light is called unpolarised light.
Now, when, because of any reason, if the direction of vibration of electric and magnetic vectors is confined to a particular direction, then such a light is called polarized light.
Polarization can occur due to various reasons. In this particular question, we will discuss polarization due to scattering.
(a) Sunlight is an unpolarised light. When this light falls on some particle, it gets scattered in different directions.
Observe the diagram

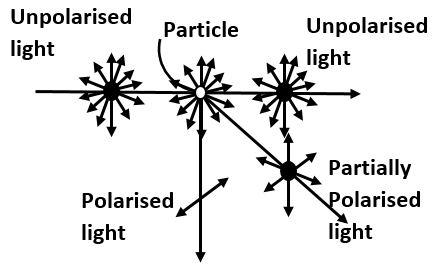
From the above diagram, we can observe that, when light falls on some particle, it scatters in the different direction. Depending on the extent of scattering, the polarization of light takes effect. If the light goes undeviated after falling on the particle, then there is no change in the polarization. The effect of polarization keeps on increasing the angle of deviation with respect to the initial direction of light. Maximum polarization occurs, that is, we get a completely polarised light at the angle of ${90^0}$ with respect to the initial direction of the light.
(b) Now let us assume that there are three polaroids. Out of which, ${P_1}$ and ${P_2}$ are placed in such a way that their axes are perpendicular to each other. And then, a polaroid, ${P_3}$ is placed in between them in such a way that it makes an angle ${45^0}$ with the axis of ${P_1}$, which obviously means that it will make an angle of ${45^0}$ with the axis of ${P_2}$ as well.
Observe the diagram

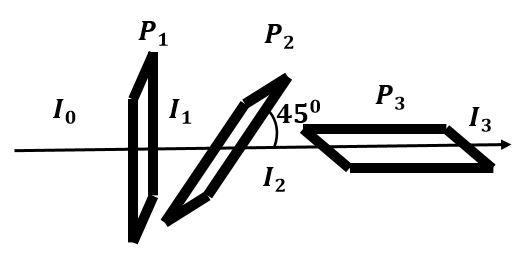
Let the initial intensity of the light be ${I_0}$
And ${I_1},$ ${I_2},$ ${I_3}$ be the intensities of light after passing through polaroids, ${P_1},$ ${P_2},$ and ${P_3}$ respectively.
Cleary, when the unpolarised light of intensity ${I_0}$ will pass through the polaroid ${P_1}$, as the axis of ${P_1}$ is vertical, only the vertical component of light will be able to pass through it. That means, the intensity of light will reduce to half.
$ \Rightarrow {I_1} = \dfrac{{{I_0}}}{2}$ . . . (1)
Now, the intensity of light after passing through a polaroid is given by Malu’s law as,
$I = {I_0}{\cos ^2}\theta $
Where,
${I_0}$ is the initial intensity of light.
\[I\] is the intensity of light after passing through a polaroid
$\theta $ is the angle between the axis of polaroids.
Using the above law, we can say that the intensity of the light after passing through the polaroid ${P_2}$ will be,
${I_2} = {I_1}{\cos ^2}\theta $
By substituting the values of ${I_1}$ and $\theta, $ we get
${I_2} = \dfrac{{{I_0}}}{2}{\cos ^2}{45^0}$
$ \Rightarrow {I_2} = \dfrac{{{I_0}}}{2}{\left( {\dfrac{1}{{\sqrt 2 }}} \right)^2}$
$ \Rightarrow {I_2} = \dfrac{{{I_0}}}{2} \times \dfrac{1}{2}$
$ \Rightarrow {I_2} = \dfrac{{{I_0}}}{4}$ . . . (2)
Again using the same formula, we can say that the intensity of the light after passing through the polaroid ${P_3}$ will be
${I_3} = {I_2}{\cos ^2}\theta $
By substituting the values of ${I_2}$ and $\theta $, we get
${I_3} = \dfrac{{{I_0}}}{4}{\cos ^2}{45^0}$
$ \Rightarrow {I_3} = \dfrac{{{I_0}}}{4}{\left( {\dfrac{1}{{\sqrt 2 }}} \right)^2}$
$ \Rightarrow {I_3} = \dfrac{{{I_0}}}{4} \times \dfrac{1}{2}$
$ \Rightarrow {I_3} = \dfrac{{{I_0}}}{8}$ . . . (3)
Therefore, from equation, (1), (2) and (3), we can conclude that the intensity of light passing through the polaroids, ${P_1},$ ${P_2}$ and ${P_3}$ will be $\dfrac{{{I_0}}}{2},$ $\dfrac{{{I_0}}}{4}$ and $\dfrac{{{I_0}}}{8}$ respectively.

Note:
Polarization of light can occur due to polarizer, polaroid, scattering, reflection or refraction.
If the polarization of light is confined to a particular plane, then it is called plane polarized light. There is also circularly polarized light. Sunlight is unpolarised light before it gets into contact with earth’s atmosphere. But it is not necessary that every ray of light that comes into contact with the earth’s atmosphere goes under polarization.