Question

A short bar magnet is placed in the magnetic meridian of the earth with the North Pole pointing north. Neutral points are found at a distance of 30 cm from the magnet on the East – West line, drawn through the middle point of the magnet. The magnetic moment of the magnet $A{m^2}$ is close to (Given $\dfrac{\mu }{{4\pi }} = {10^{ - 7}}$ in SI units and ${B_H} = $ Horizontal component of earth’s magnetic field $ = 3.6 \times {10^{ - 5}}Tesla.$)
(A). 4.9
(B). 14.6
(C). 19.4
(D). 9.7

Answer 1

Hint: Neutral points are points where the net magnetic field due to two magnetic sources is zero. In our case, the two sources are earth’s magnetic field and bar magnet’s magnetic field. Magnetic field is directly related to the magnetic moment.

Formula used:
Magnetic field due to a bar magnet is given as
$$B = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{m}{{{r^3}}}$$
$\dfrac{{{\mu _0}}}{{4\pi }} = {10^{ - 7}}$
where m is the pole strength of the bar magnet,
r is the radial distance from the magnet.

Complete step-by-step answer:
We are given a bar magnet which is placed in the magnetic meridian of Earth. The magnetic meridian is line on the surface of Earth which is in the same direction as that of the horizontal component of Earth’s magnetic field.
The neutral points are situated at a distance of 30 cm from the bar magnet along the east-west line drawn through the middle point of the bar magnet.

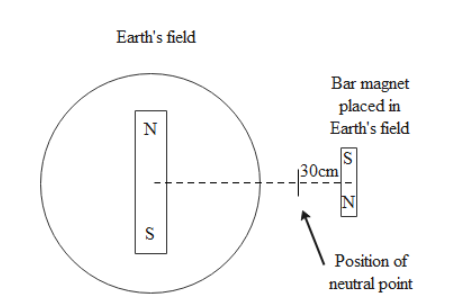
$ r = 30cm = \dfrac{{30}}{{100}}m = 0.3m \\
  \dfrac{{{\mu _0}}}{{4\pi }} = {10^{ - 7}} \\ $
Magnetic moment is basically the strength of the magnetic field of a magnet. In our case, we can calculate it by using the information related to the neutral points as follows: Net magnetic field is zero at neutral points so,
${\overrightarrow B _{magnet}} = {\overrightarrow B _{earth}}$

Using the formula for magnetic field and putting various values, we get
${\overrightarrow B _{earth}} = {10^{ - 7}}\dfrac{m}{{{{(0.3)}^3}}}$

Since the bar magnet is placed in the magnetic meridian of Earth, the magnetic field due to Earth is equal to the horizontal component of Earth’s magnetic field which has the following value.
$ {\overrightarrow B _{earth}} = {B_H} = 3.6 \times {10^{ - 5}}tesla \\
  \therefore 5 \times {10^{ - 4}} = {10^{ - 7}}\dfrac{m}{{{{(0.3)}^3}}} \\
   \Rightarrow m = \dfrac{{3.6 \times {{10}^{ - 5}} \times {{(0.3)}^3}}}{{{{10}^{ - 7}}}} \\
   \Rightarrow m = 9.72Am $

Hence, the correct answer is option D.

Note: The value of Earth’s magnetic field is different at different points on Earth. If the magnet is not aligned with the magnetic meridian of Earth then the magnetic field due to Earth is not equal to the horizontal component and needs to be calculated separately.