Question

A ship $A$ is moving westwards with a speed of $10km{{h}^{-1}}$ and a ship $B$, $100km$ south of $A$, is moving northwards with a speed of $10km{{h}^{-1}}$. The time after which the distance between them becomes the shortest is
$\begin{align}
  & A)5\sqrt{2}h \\
 & B)10\sqrt{2}h \\
 & C)0h \\
 & D)5h \\
\end{align}$

Answer 1

Hint: A well labelled diagram is drawn to understand the given question. Distances travelled by both the ships at a particular instant is determined. Distance is equal to the product of speed and time. The time after which the distance between the ships becomes the shortest is determined by equating the first differential of distance with respect to time, to zero.

Formula used:
$1){{d}_{A/B}}={{v}_{A/B}}\times t$
$2)d=\sqrt{{{d}_{A}}^{2}+{{d}_{Q}}^{2}}$
\[3)\dfrac{d(d)}{dt}=0\]

Complete step-by-step answer:
We are given that ship $A$ moves westwards with a speed of $10km{{h}^{-1}}$ and a ship $B$, $100km$ south of $A$, moves northwards with a speed of $10km{{h}^{-1}}$, as shown in the following figure. We are required to determine the time after which the distance between them becomes the shortest.

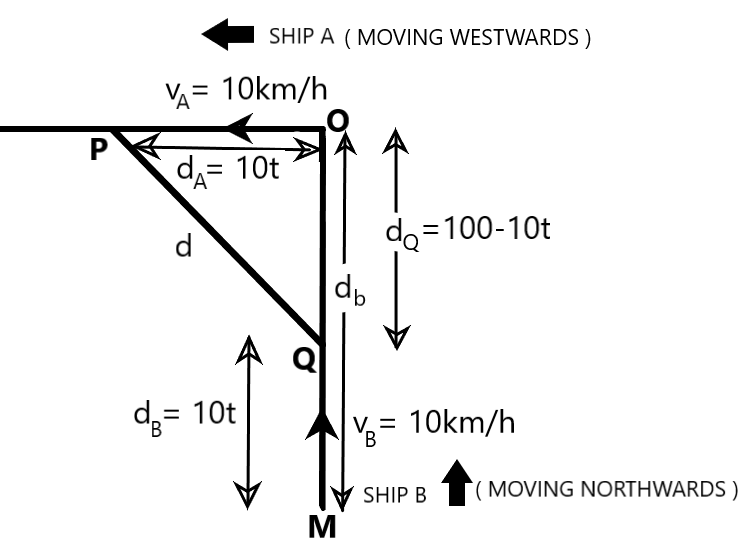
Suppose the ships $A$ and $B$ have travelled distances ${{d}_{A}}$ and ${{d}_{B}}$ in a particular time, say, $t$. Clearly, ${{d}_{A}}$ and ${{d}_{B}}$ are given by
$\begin{align}
  & {{d}_{A}}={{v}_{A}}\times t=10t \\
 & {{d}_{B}}={{v}_{B}}\times t=10t \\
\end{align}$
where
${{v}_{A}}={{v}_{B}}=10km{{h}^{-1}}$, are the velocities of ship $A$ and ship $B$ respectively
Let this set of equations be denoted as X.
From the figure, it is clear that
$\begin{align}
  & {{d}_{A}}=10t=PO \\
 & {{d}_{B}}=10t=MQ \\
 & {{d}_{Q}}={{d}_{b}}-{{d}_{B}}=100-10t=QO \\
\end{align}$
where
${{d}_{Q}}$ is the distance between the starting point of ship $A$and the point at which ship $B$ is positioned, at time $t$
${{d}_{b}}=100km$ is the distance between ship $A$ and ship $B$ at $t=0$ (given)
Now, if $d$ represents the distance between ship $A$ and ship $B$ at time $t$, then, from the right triangle $POQ$, $d$ is given by
${{d}^{2}}=P{{Q}^{2}}=O{{P}^{2}}+O{{Q}^{2}}\Rightarrow {{d}^{2}}={{d}_{A}}^{2}+{{d}_{Q}}^{2}\Rightarrow d=\sqrt{{{d}_{A}}^{2}+{{d}_{Q}}^{2}}$
Let this be equation 2.
Substituting the values of ${{d}_{A}}$ and ${{d}_{Q}}$ in equation 2, we have
\[d=\sqrt{{{d}_{A}}^{2}+{{d}_{B}}^{2}}\Rightarrow d=\sqrt{{{(10t)}^{2}}+{{(100-10t)}^{2}}}=\sqrt{200{{t}^{2}}+10000-2000t}\]
Let this be equation 3.
Clearly, from equation 3, we can understand that distance between the ships is represented as a function of time. To obtain the minimum value of $d$ or the shortest distance between the ships, we can equate equation 3 to zero, with respect to time as given below:
\[\dfrac{d(d)}{dt}=0\Rightarrow \dfrac{d\left( \sqrt{200{{t}^{2}}+10000-2000t} \right)}{dt}=0\Rightarrow \dfrac{400t-2000}{2\sqrt{200{{t}^{2}}+10000-2000t}}\Rightarrow t=\dfrac{2000}{400}=5\]
Let this be equation 4.
Therefore, the time after which the distance between the ships becomes the shortest is $5h$. Hence, the correct answer is option $D$.

So, the correct answer is “Option D”.

Note: It can be clearly understood that all the units are matching and conversions are not required here. Substituting equation 4 in equation 3, we have
\[{{d}_{\min }}=\sqrt{200{{t}^{2}}+10000-2000t}\Rightarrow d=\sqrt{200\times 25+10000-2000\times 5}=\sqrt{5000}=70.71km\]
where
${{d}_{\min }}$ is the shortest distance between the ships.
From the above explanation, it is clear that the calculated time can also be utilised to determine the shortest distance between the ships in their course of journey.