Question

A ship A is moving Westwards with a speed of \[10km/h\] and a ship B \[100km\] South of A is moving northwards with a speed of \[10km/h\]. The time after which the distance between them becomes shortest is:
 \[\begin{align}
  & A)0h \\
 & B)5h \\
 & C)5\sqrt{2}h \\
 & D)10\sqrt{2}h \\
\end{align}\]

Answer 1

Hint: Here, the velocities of ships A and B are given. From this, we can find the velocity of A with respect to B. Then, draw a vector diagram and mark the distances and angles. Consider the triangle made by the resultant velocity and the path of ship B and find out all the sides and thereby the time taken by the ships to reach their shortest distance can be calculated.
Formula used:
 \[\text{time = }\dfrac{\text{distance}}{\text{velocity}}\]

Complete step by step answer:

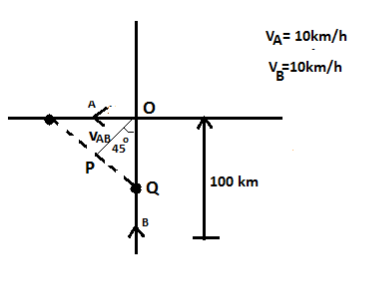
 Velocity of A with respect to B is,
 \[{{\vec{v}}_{AB}}={{\vec{v}}_{A}}-\left( -{{{\vec{v}}}_{B}} \right)={{\vec{v}}_{A}}+{{\vec{v}}_{B}}\]
 Then,
 \[{{v}_{AB}}=\sqrt{{{v}_{A}}+{{v}_{B}}}\] ------- 1
 Given that,
 Velocity of A, \[{{v}_{A}}=10km/h\]
Velocity of B, \[{{v}_{B}}=10km/h\]
 Substitute the velocities of ships A and B in equation 1 we get,
 Velocity of A with respect to B, \[{{v}_{AB}}=\sqrt{{{10}^{2}}+{{10}^{2}}}=10\sqrt{2}\]
 From the above diagram the shortest distance between ships A and B is PQ.
Consider triangle POQ,
 \[\sin 45=\dfrac{PQ}{OQ}\]
 \[OQ=100km\]
 Then,
 \[PQ=OQ\times \sin 45=100\times \dfrac{1}{\sqrt{2}}=50\sqrt{2}m\]
 We have, \[\text{time = }\dfrac{\text{distance}}{\text{velocity}}\]
Substitute the values of PQ and \[{{v}_{AB}}\]in the above equation, we get,
Then, the time taken to reach the shortest distance,
\[t=\dfrac{PQ}{{{v}_{AB}}}=\dfrac{50\sqrt{2}}{10\sqrt{2}}=5h\]

Therefore, the answer is option B.

Note:
Alternate method to solve the question

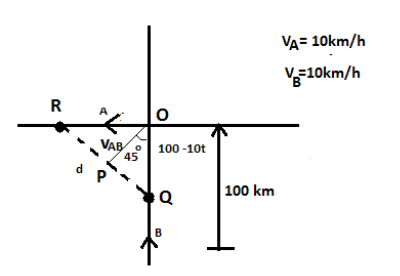
Given,
Velocity of A, \[{{v}_{A}}=10km/h\]
Velocity of B, \[{{v}_{B}}=10km/h\]
Given that, both ships A and B are travelling with the same velocity. Then, at any instant \[t\] the distance traveled by the ships will be the same.
i.e.,
Distance travelled by ship A = Distance travelled by ship B \[=10t\]
Then, the remaining distance for B is, \[100-10t\].
Then, considering triangle ROQ,
\[{{d}^{2}}=P{{O}^{2}}+O{{Q}^{2}}\]
\[{{d}^{2}}={{\left( 10t \right)}^{2}}+{{\left( 100-t \right)}^{2}}\]
\[d=\sqrt{100{{t}^{2}}+10000+100{{t}^{2}}-200t}=\sqrt{200{{t}^{2}}+10000-2000t}\]
 Differentiating both sides with respect to time,
\[\dfrac{d\left( d \right)}{dt}=0\]
\[\Rightarrow 0=400t-2000\]
\[\Rightarrow 400t=2000\]
\[\Rightarrow t=5hr\]