Question

A shell of mass 20Kg at rest explodes into two fragments whose masses are in the ratio 2:3. The smaller fragment moves with a velocity of 6m/s. The kinetic energy of the larger fragment is
$
  (a){\text{ 96J}} \\
  (b){\text{ 216J}} \\
  (c){\text{ 144J}} \\
  (d){\text{ 360J}} \\
 $

Answer 1

Hint – In this question let the smaller fragment be of mass ${m_1}$ Kg and the larger fragment be of mass ${m_2}$ Kg. Use the constraint provided in the question to get the value of individual masses for smaller as well as larger fragments. Then apply the law of conservation of momentum that is the initial momentum of the system must be equal to the final momentum. This will help get the right answer.
Step by step answer:

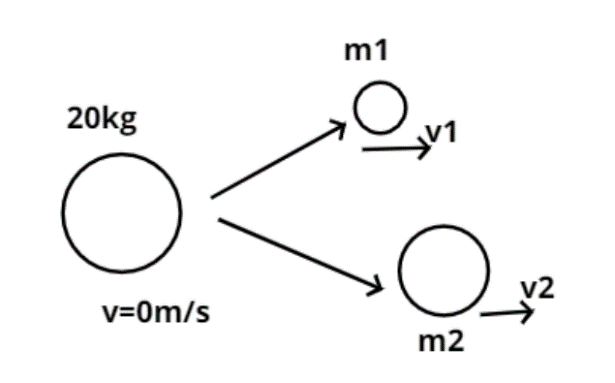
Given weight of the shell is = 20 Kg.
Now this explodes into two fragments whose masses are in the ratio 2 : 3.
Let the smaller fragment mass be ${m_1}$ Kg and the larger fragment mass be ${m_2}$ Kg.
Therefore, ${m_1} + {m_2} = 20$ Kg..................... (1)
And $\dfrac{{{m_1}}}{{{m_2}}} = \dfrac{2}{3}$
$ \Rightarrow {m_1} = \dfrac{2}{3}{m_2}$
Now substitute this value in equation (1) we have,
$ \Rightarrow \dfrac{2}{3}{m_2} + {m_2} = 20$
Now simplify this equation we have,
$ \Rightarrow \dfrac{5}{3}{m_2} = 20$
$ \Rightarrow {m_2} = \dfrac{{20\left( 3 \right)}}{5} = 12$Kg.
Now from equation (1) we have,
$ \Rightarrow {m_1} + 12 = 20$
$ \Rightarrow {m_1} = 20 - 12 = 8$ Kg.
Now it is given that the smaller fragment moves with a velocity (${v_1}$) of 6m/s.
Now according to conservation of momentum we have,
Summation of the Product of the mass and the velocity of the two exploded balls is zero as initially when the 20Kg mass explodes it was at rest so the initial velocity of the system was 0, thus initial momentum that is$Mv = 20 \times 0 = 0$.
Let the velocity of the larger fragment be ${v_2}$m/s and the velocity of the smaller fragment be ${v_1}$m/s
So $Mv = {m_1}{v_1} + {m_2}{v_2}$
$ \Rightarrow {m_1}{v_1} + {m_2}{v_2} = 0$
Now substitute the values in the above equation we have,
$ \Rightarrow 8\left( 6 \right) + 12\left( {{v_2}} \right) = 0$
$ \Rightarrow {v_2} = - \dfrac{{48}}{{12}} = - 4$ m/s, (negative sign indicates that the larger fragment goes into opposite side w.r.t the smaller fragment)
Now as we know that the kinetic energy is given as (K.E) = $\dfrac{1}{2}m{v^2}$
So the kinetic energy of the larger fragment is
$ \Rightarrow K.E = \dfrac{1}{2}{m_2}v_2^2$
Now substitute the values in the above equation we have,
$ \Rightarrow K.E = \dfrac{1}{2}\left( {12} \right){\left( { - 4} \right)^2} = 6\left( {16} \right) = 96J$
So this is the required kinetic energy of the larger fragment.
Hence option (A) is the correct answer.

Note – The rockets are a great example of conversation of momentum as when the rocket takes off some gases are ejected through its vessels, since the molecules of these gases after combustion attains high energy thus possess velocities and thus momentum. This momentum is what provides the forward thrust or the momentum as it is always conserved.