Question

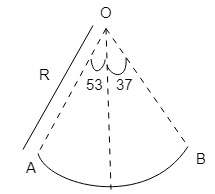
A section of fixed smooth circular track of radius $R$ in the vertical plane is shown in the figure. A block is released from position $A$ and leaves the track at$B$. The radius of curvature of its trajectory just after it leaves the track at $B$ is?
$(A)R$
$(B)\dfrac{R}{4}$
$(C)\dfrac{R}{2}$
$(D)\dfrac{R}{3}$

Answer 1

Hint: This question is based on the concept of law of conservation of energy. We will apply the law of conservation of energy at the two points A and B, and we will get a relation between them. Also, since the block leaves at the point B, the normal force will be equal to zero.

Complete step by step answer:
In this question, we are given that the radius of the track is$R$.
For this particular geometry, we can say that,
$x = R(1 - \cos {53^o})$
On solving this, we get,
$x = 0.4R.....(1)$
We can also say that,
$y = R(1 - \cos {37^o})$
$y = 0.2R......(2)$
On applying the law of conservation of energy at the points A and B,
$mg(0.4R) = mg(0.2R) + \dfrac{1}{2}m{v^2}$
On cancelling $m$ o both the sides,
$g(0.4R) = g(0.2R) + \dfrac{1}{2}{v^2}$
On further solving, we get,
${v^2} = 0.4gR$
Since, the block leaves the block at the point B,
So, $N = 0$
$\dfrac{{m{v^2}}}{r} = mg\cos {37^o}$
$\dfrac{{m \times 0.4gR}}{r} = mg(0.8)$
On solving this further, we get,
$r = \dfrac{R}{2}$
So, the final answer is $(C)\dfrac{R}{2}$.

Additional information:
Some basic applications of the law of conservation of energy are:
1) When a car hits another car in an accident to make it move, then the transformation of energy takes place from one car to another.
2) Water is very often used to produce electricity. When water falls from the sky, the conversion of potential energy to kinetic energy takes place. This energy is then used to rotate the turbine of a generator, which is a part of the hydroelectricity setup, to produce electricity. In this particular process, the potential energy of water in a dam is converted into kinetic energy which can then be used to produce electric energy.

Note:
Circular motion is defined as the movement of a body along the circumference of a circle or its rotation along a circular field. Since the velocity vector of the object is constantly changing direction, the moving object is undergoing acceleration by a force known as the centripetal force which acts in a direction of the centre of rotation.