Question

A scientist measures the time period of a simple pendulum as T in a lift at rest. If the lift moves up with an acceleration equal to one-fourth of the acceleration of gravity, the new time period is

A. \[\dfrac{T}{4}\]
B. \[4T\]
C. \[\dfrac{2}{\sqrt{5}}T\]
D. \[\dfrac{\sqrt{5}}{2}T\]

Answer 1

Hint: Here the varying quantity is acceleration. According to the simple pendulum concept, the time period of the simple pendulum depends only on the acceleration and length of the pendulum. Since the acceleration is in the denominator of the equation of time period, when the acceleration increases the time period decreases.
Formula used: Time period of a simple pendulum is, \[T=2\pi \sqrt{\dfrac{L}{g}}\], where L is the length of the simple pendulum and g is the acceleration due to gravity.

Complete step by step answer:
 To find the new time period of the simple pendulum, we can redraw the figure given in the question. We can consider the length of the simple pendulum as L. At the rest, the only acceleration acting on the body is an acceleration due to gravity. That is, g. But the lift starts to move upwards with an acceleration of \[\dfrac{g}{4}\]. Thus the total acceleration of the pendulum will be the sum of acceleration due to gravity and the acceleration of the lift.

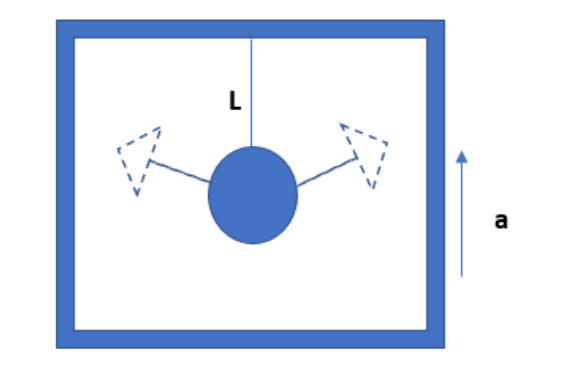
The time period of a simple pendulum at rest will be,
\[T=2\pi \sqrt{\dfrac{L}{g}}\], where L is the length of the simple pendulum and g is the acceleration due to gravity.
When the lift starts to move upwards, the acceleration of the lift becomes \[\dfrac{g}{4}\]. So we have to add this acceleration also with the acceleration due to gravity to get the total acceleration of the simple pendulum.
Total acceleration will be,
\[a=g+\dfrac{g}{4}\]
\[a=\dfrac{5g}{4}\]
We can plug this acceleration in the equation of time period to find the new time period.
\[{{T}_{n}}=2\pi \sqrt{\dfrac{L}{a}}\]
\[{{T}_{n}}=2\pi \sqrt{\dfrac{4L}{5g}}\]
We can compare the new time period with the initial time period.
\[{{T}_{n}}=\sqrt{\dfrac{4}{5}}T\]
It can simplify as,
\[{{T}_{n}}=\dfrac{2}{\sqrt{5}}T\], Hence the correct option is C.
Note: Motion in a lift is always a special case. Here the acceleration of the lift will bring great impact to the motion. Here we are adding the acceleration of the lift to the acceleration due to gravity since the lift moves upwards. If the lift is moving downward, we have to reduce the acceleration of the lift from the acceleration due to gravity.
The normal force acting on the body from the lift at various conditions are;
1. \[N=mg\], when the lift is at rest or moving with a constant velocity.
2. \[N=mg+ma\], when the lift moves upward with an acceleration.
3. \[N=mg-ma\], when the lift moves downward with an acceleration.
The normal force is equal to your weight. So, you will feel heavier when the lift moves upward with an acceleration a and lighter when the lift moves downward with an acceleration a.