
A satellite of mass
Answer
515.1k+ views
Hint: Remember that for a satellite to stay in orbit there should be a balance between the gravitational and the centrifugal forces that it is subjected to. Additionally, by assuming that the satellite orbit traces a circular perimeter and calculating the orbiting velocity of the satellite from the balance of the abovementioned forces you can find the time period.
Formula used:
Centrifugal force:
Gravitational force:
In general, for a circular orbit, time period
Complete step by step answer:
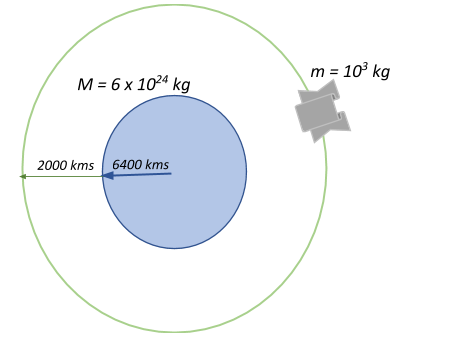
Let us look at the forces that are acting on a satellite orbiting the earth.
Firstly, there is the earth’s gravitational force that tugs on the satellite and pulls it closer:
Secondly, due to the circular motion of the satellite it experiences a centrifugal force that pushes that satellite away:
Now the satellite maintains its orbit by balancing the gravitational force and the centrifugal force. At equilibrium
Here,
Therefore,
Now, for a circular orbit, time period
Therefore, the time period of revolution for the satellite is 2.12 hrs.
Note:
Always remember to include the Earth’s radius in addition to the distance of the satellite from the Earth’s surface while considering orbital radius as the magnitude of influence of Earth’s gravity depends on the distance of the satellite from the orbiting centre which is the centre of the Earth.
Proceed cautiously while converting km or
Formula used:
Centrifugal force:
Gravitational force:
In general, for a circular orbit, time period
Complete step by step answer:

Let us look at the forces that are acting on a satellite orbiting the earth.
Firstly, there is the earth’s gravitational force that tugs on the satellite and pulls it closer:
Secondly, due to the circular motion of the satellite it experiences a centrifugal force that pushes that satellite away:
Now the satellite maintains its orbit by balancing the gravitational force and the centrifugal force. At equilibrium
Here,
Therefore,
Now, for a circular orbit, time period
Therefore, the time period of revolution for the satellite is 2.12 hrs.
Note:
Always remember to include the Earth’s radius in addition to the distance of the satellite from the Earth’s surface while considering orbital radius as the magnitude of influence of Earth’s gravity depends on the distance of the satellite from the orbiting centre which is the centre of the Earth.
Proceed cautiously while converting km or
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

How much is 23 kg in pounds class 11 chemistry CBSE




