Question

A satellite is revolving in a circular orbit at a height h from the earth surface (radius of earth$Rh < < R$). The minimum increase in its orbital velocity required so that the satellite could escape from the earth gravitational field, is close to: (Neglect the effect of atmosphere.)
A. $\sqrt {gR} $
B. $\sqrt {gR/2} $
C. $\sqrt {gR} \left( {\sqrt 2 - 1} \right)$
D. $\sqrt {2gR} $

Answer 1

Hint:1. The velocity at which a body (here satellite) starts revolving around the other body (here earth), then this velocity is known as orbital velocity,
${v_o} = \sqrt {\dfrac{{GM}}{r}} = \sqrt {\dfrac{{GM}}{{R + h}}} $
For near satellite
$h < < R \Rightarrow R + h \simeq R$
${v_o} = \sqrt {\dfrac{{GM}}{R}} = \sqrt {\dfrac{{g{R^2}}}{R}} \,\,\,\,\,\,\,\,\,\,\left[ {\because g = \dfrac{{GM}}{{{R^2}}}} \right]$
${v_o} = \sqrt {gR} .$
2. The minimum velocity that is required to a body (here satellite) to project it at infinity i.e. at outside the gravitational pull of another body (here earth) known as, escape velocity.
${v_e} = \sqrt {\dfrac{{2GM}}{r}} = \sqrt {\dfrac{{2GM}}{{R + h}}} $
For a near satellite
$h < < R \Rightarrow R + h \simeq R$
So, ${v_e} = \sqrt {\dfrac{{2GM}}{R}} = \sqrt {\dfrac{{2g{R^2}}}{R}} \,\,\,\left[ {\because g = \dfrac{{GM}}{{{R^2}}}} \right]$
${v_e} = \sqrt {2gR} $

Complete Step by Step Answer:

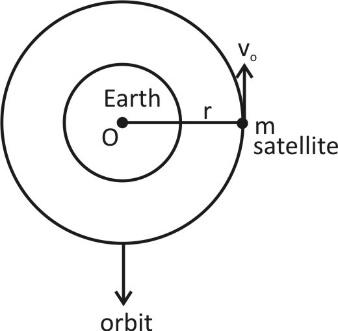
For a satellite which is orbiting with velocity ${v_o}.$The gravitational pull by earth is balanced by centripetal force so, gravitational pull by earth $ = $ centripetal force
 So, $\dfrac{{GMm}}{{{r^2}}} = \dfrac{{mv_{^o}^2}}{r}$
Or ${v_o} = \sqrt {\dfrac{{GM}}{r}} $
Here, $r = R + h$
For a satellite to escape, the total final energy of the satellite must be zero. Let escape velocity of satellite at height h be \[{v_e}.\]
Then, By mechanical energy conservation
${K_i} + {U_i} = {K_f} + {U_f}$
$\dfrac{1}{2}mv_e^2 + \dfrac{{ - GMm}}{r} = 0 + 0$
Or, $\dfrac{1}{2}mv_e^2 + \dfrac{{GMm}}{r}$
${v_e} = \sqrt {\dfrac{{2GM}}{r}} $
The difference is velocities is given by, $\Delta v = {v_e} - {v_o}$
$\Delta v = \sqrt {\dfrac{{2GM}}{r}} - \sqrt {\dfrac{{GM}}{r}} $
Or, $\Delta v = \sqrt {\dfrac{{GM}}{r}} \left( {\sqrt 2 - 1} \right)$
We know, \[g = \dfrac{{GM}}{{{r^2}}}\] [at orbital height]
Or, $GM = g{r^2}$
\[\Delta v = \sqrt {\dfrac{{g{r^2}}}{r}} \left( {\sqrt 2 - 1} \right)\]
$\Delta v = \sqrt {gr} \left( {\sqrt 2 - 1} \right)$
$\because \,r = R + h,$
For near satellite i.e. $h < < R,$ therefore $h + R \simeq R$
So, $r \simeq R$
So, \[\Delta v \simeq \sqrt {gR} \,\left( {\sqrt 2 - 1} \right)\]
Hence, option (C) is correct.

Note:So, By trick for a near satellite $\left( {h < < R} \right)$ orbital velocity, ${v_o} = \sqrt {gR} $ and escape velocity, ${v_e} = \sqrt {2gR} $. Hence the minimum increase in orbital velocity of satellite so that it could escape from the earth’s gravitational field is,
$\Delta v \simeq {v_e} - {v_o}$
$\Delta v \simeq \sqrt {2gR} - \sqrt {gR} $
$\Delta v \simeq \sqrt {gR} \left( {\sqrt 2 - 1} \right)$.