Question

A saree is 5m long and 1.5m wide. A border of 20cm width is printed along its four sides. Find the cost of printing the border at Rs.3 per square meter.

Answer 1

Hint: In this question it is given that a saree is 5m long and 1.5m wide. A border of 20cm width is printed along its four sides. We have to find the cost of printing the border at Rs.3 per square meter.
So to understand it we have to draw the diagram,

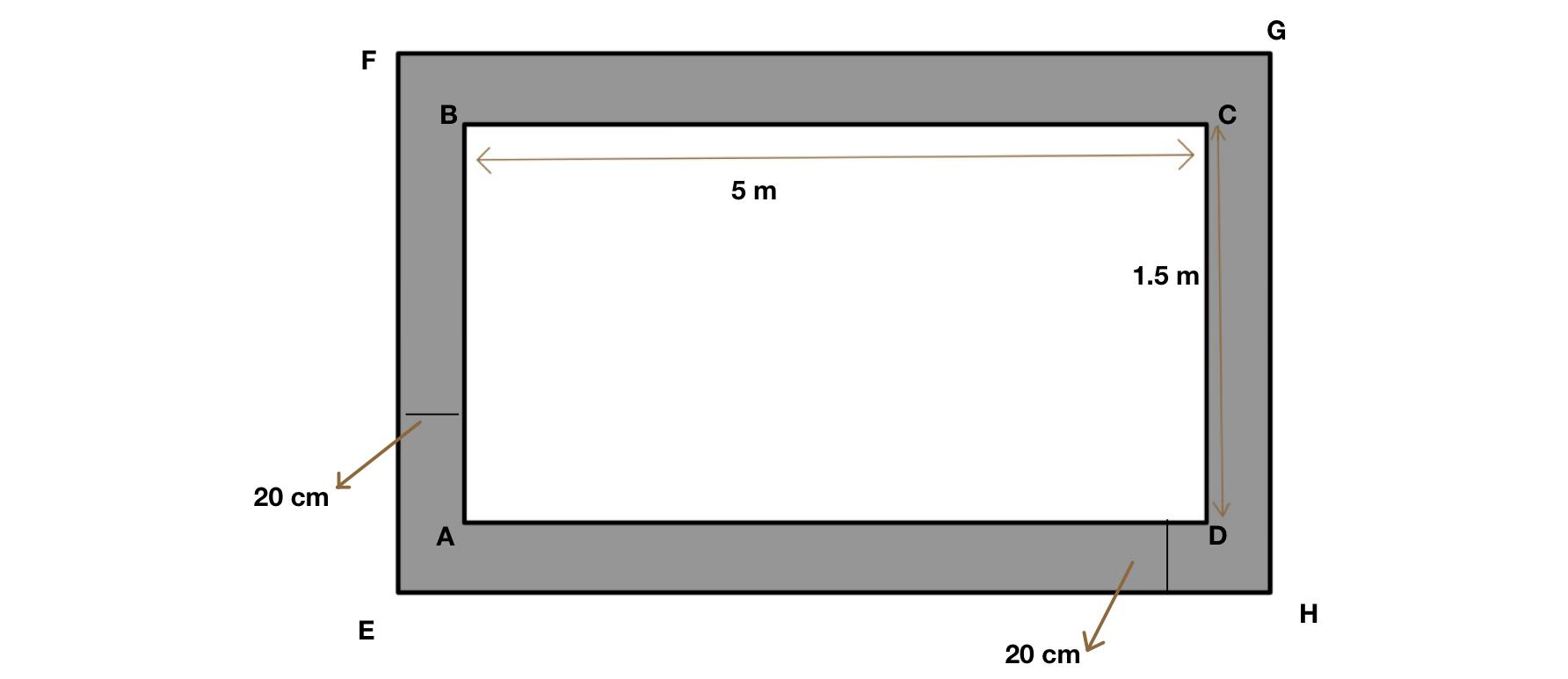
So we are considering EFGH is a rectangular saree of length 5 m and width 1.5 m. So to find the cost of the border we need to first find the area of the border(shaded portion).
So from the diagram,
The area of shaded portion = area of EFGH -area of ABCD
Where area of a rectangle= length$\times$width

Complete step-by-step answer:
Here it is given, the length of the saree =FG=EH=5 m, and width=EF=GH=1.5 m
Therefore, the area of the rectangle EFGH
= length$\times$width=$FG\times EF$ = $5\times 1.5\ m^{2}=7.5\ m^{2}$
The width of the border= 20 cm =$$\dfrac{20}{100}$$=0.2 m
Now after bordering, the length of the remaining portion
i.e AD=BC=$(FG-2\times 0.2)$=$(5-2\times 0.2)$ m=4.6 m
And the width = AB=CD=$(EF-2\times 0.2)$= $(1.5-2\times 0.2)$=1.1 m
Therefore, the area of ABCD
=length$\times$width=$BC\times AB$=$4.6\times 1.1\ m^{2}=5.06\ m^{2}$

Therefore, the area of the bordered portion = area of EFGH -area of ABCD=$\left( 7.5-5.06\right) m^{2}=2.44\ m^{2}$
Also given the cost of printing the border is Rs.3 per square meter
i,e, The cost of 1 $m^{2}$ printing =Rs 3
$\therefore$ the cost of 2.44 $m^{2}$ printing = Rs $3\times 2.44$ =Rs 7.32
Hence, the cost of printing the border at Rs.3 per square meter is Rs 7.32.


Note: While calculating the length of the inner portion we subtracted two times the width of the border because as you can see the printed portion occupies the same width in each of the sides of length and breath, so for right and left side we have to subtract two times.