Question

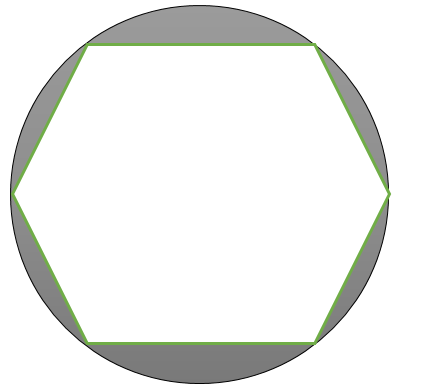
A round table cover has six equal designs as shown in the figure. If the radius of the cover is 28 cm, find the cost making the design t the rate of \[{\text{Rs}}{\text{.3}}{\text{.50 per c}}{{\text{m}}^2}\].\[\left( {{\text{Use }}\sqrt 3 = 1.7} \right)\].

A. Rs. 1145.3
B. Rs. 1348
C. Rs. 1626.8
D. Rs. 1723.5

Answer 1

Hint: First of all, find the area of the sector formed by one design and area of one design. Then find the area of the round table which is given by the difference of the area of the six sectors and are of the six designs. And then multiply it with the cost of making the design per unit area to obtain the required answer.

Complete step-by-step solution -
Let the radius of the round table cover be \[r = 28{\text{ cm}}\]
As the round table cover has six equal designs, the angles made with the designs to the centre of the circle is also divided into six as shown in the below figure:

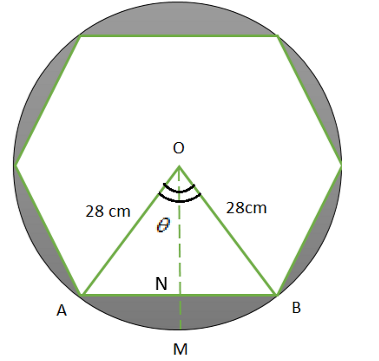
Therefore, \[\theta = \dfrac{{{{360}^0}}}{6} = {60^0}\]
We know that the area of the sector formed by the circle with radius \[r\] with an angle \[\theta \] is given by \[\dfrac{\theta }{{{{360}^0}}} \times \pi {r^2}\]
Therefore, the area formed by the sector \[OAMB = \dfrac{{{{60}^0}}}{{{{360}^0}}} \times \dfrac{{22}}{7} \times 28 \times 28 = 410.67{\text{ c}}{{\text{m}}^2}\]
Now, in \[\Delta ONA\] and \[\Delta ONB\]
\[
   \Rightarrow \angle ONA = \angle ONB{\text{ }}\left[ {{\text{each 9}}{{\text{0}}^0}} \right] \\
   \Rightarrow OA = OB{\text{ }}\left[ {{\text{radii of common circle}}} \right] \\
   \Rightarrow ON = ON{\text{ }}\left[ {{\text{common}}} \right] \\
  \therefore \Delta ONA \cong \Delta ONB{\text{ }}\left[ {{\text{By RHS congruency}}} \right] \\
\]
Hence, clearly \[AN = NB = \dfrac{1}{2}AB\]
And \[\angle AON = \angle BON = \dfrac{1}{2}\angle AOB = \dfrac{{{{60}^0}}}{2} = {30^0}\]
Now, in \[\Delta ONA\] consider
\[
   \Rightarrow \cos {30^0} = \dfrac{{ON}}{{OA}} \\
   \Rightarrow \dfrac{{\sqrt 3 }}{2} = \dfrac{{ON}}{{28}} \\
  \therefore ON = 14\sqrt 3 {\text{ cm}} \\
\]
And
\[
   \Rightarrow {\text{sin3}}{{\text{0}}^0} = \dfrac{{AN}}{{OA}} \\
   \Rightarrow \dfrac{1}{2} = \dfrac{{AN}}{{28}} \\
  \therefore AN = 14{\text{ cm}} \\
\]
We know that the area of the triangle formed with base \[b\] and height \[h\] is given by \[\Delta = \dfrac{1}{2} \times b \times h\]
So, area of the \[\Delta AOB = \dfrac{1}{2} \times AB \times ON = \dfrac{1}{2} \times 28 \times 14\sqrt 3 = 196\sqrt 3 = 196\left( {1.7} \right) = 333.2{\text{ c}}{{\text{m}}^2}\]
Hence area of one design = area of sector \[OAMB\] - area of \[\Delta AOB\]
                                               = \[410.67 - 333.2 = 77.47{\text{ c}}{{\text{m}}^2}\]
Therefore, the area of six designs \[ = 6 \times 77.47 = 464.82{\text{ c}}{{\text{m}}^2}\]
Given cost of making the design at the rate of \[{\text{Rs}}{\text{.3}}{\text{.50 per c}}{{\text{m}}^2}\]
Hence the cost of making the designs \[ = 3.50 \times 464.82 = Rs.1626.8\]
Thus, the correct option is C. Rs. 1626.8

Note: RHS congruence rule says that if in two right triangles the hypotenuse and one side of one triangle are equal to the hypotenuse and one side of the other triangles, then the two triangles are congruent. By using congruent property we find the unknown sides.