Question

A room is 6 meters 24 centimetres in length and 4 meters 32 centimetres in width. Find the least number of square tiles of equal size required to cover the entire floor of the room?
(a) 117
(b) 222
(c) 202
(d) 353

Answer 1

Hint:Here, length and width of room is given in meter and centimetre. So, first convert it in one centimetre or meter. Further, we need to find a minimum number of tiles that covers the entire floor of the room. So, the concept of Highest common factor (HCF) will be applicable.

Complete step-by-step answer:
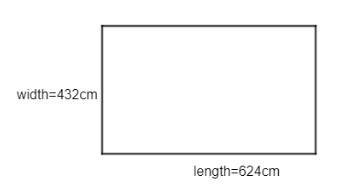
We are given a length of room as 6m 24cm which we will convert it to centimetre for easy calculation. So, we know 1m $=100$ cm. Therefore, for length 6m $=600$ cm which will be $=600+24=624cm$
Similarly, for width 4m $=400$ cm which will be $=400+32=432cm$

Now, we want the least number of tiles to cover the floor, so we need to find HCF for both length and width.
On finding H.C.F we will get:
H.C.F of 624
$\begin{align}
  & \text{ }2\left| 624 \right. \\
 & \text{ }2\left| 312 \right. \\
 & \text{ }2\left| 156 \right. \\
 & \text{ }2\left| 78 \right. \\
 & \text{ }3\left| 39 \right. \\
 & 13\left| 13 \right. \\
 & \text{ 1} \\
\end{align}$
H.C.F of 432
$\begin{align}
  & 2\left| 432 \right. \\
 & 2\left| 216 \right. \\
 & 2\left| 108 \right. \\
 & 2\left| 54 \right. \\
 & 3\left| 27 \right. \\
 & 3\left| 9 \right. \\
 & 3\left| 3 \right. \\
 & \text{ 1} \\
\end{align}$

So, HCF of both 624 and 432 we have to find by taking all the common factors together which we will get as $=2\times 2\times 2\times 2\times 3=48$
Therefore, number of tiles will be equal to
$\dfrac{(length \times width)}{(\text{HCF of 624 and 432}) \times (\text{HCF of 624 and 432})}$
$=\dfrac{\left( 624\times 432 \right)}{\left( 48\times 48 \right)}=117$
Thus, 117 square tiles are required.
Hence, option (a) is correct.

Note: Students might get confused with least common multiple (LCM) and highest common factor (HCF). So, the concept of both these terms should be clear when and where to use them correctly. The HCF defines the greatest factor present in between given two or more numbers, whereas LCM defines the least number which is exactly divisible by two or more numbers. Now, instead of HCF if LCM is done then answer will be totally different i.e.
  $\begin{align}
  & 2\left| \!{\underline {\,
  624,432 \,}} \right. \\
 & 2\left| \!{\underline {\,
  312,216 \,}} \right. \\
 & 2\left| \!{\underline {\,
  156,108 \,}} \right. \\
 & 2\left| \!{\underline {\,
  \text{ }78,\text{ }54 \,}} \right. \\
 & 3\left| \!{\underline {\,
  \text{ }39,\text{ }27 \,}} \right. \\
 & 3\left| \!{\underline {\,
  \text{ }13,\text{ }9 \,}} \right. \\
 & 3\left| \!{\underline {\,
  \text{ }13,\text{ }3 \,}} \right. \\
 & 13\left| \!{\underline {\,
  \text{ }13,\text{ }1 \,}} \right. \\
 & \text{ 1, 1} \\
\end{align}$
So, LCM $=2\times 2\times 2\times 2\times 3\times 3\times 3\times 13=5616$