
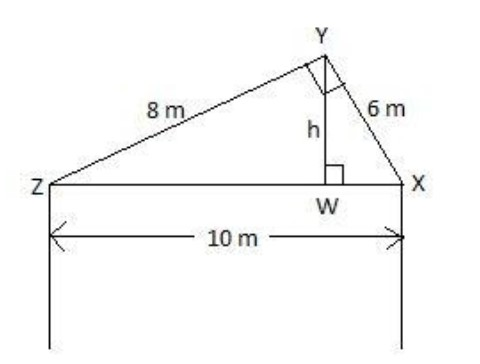
A roof has a cross-section as shown in the diagram. Find the height ‘h’ of the roof.

Answer
614.4k+ views
Hint: Find the area of the triangle using the formula: $\text{A}=\dfrac{1}{2}\times \text{base}\times \text{height}$, where ‘A’ is the area of the triangle. Consider ‘XY’ as the base and ‘ZY’ as the height of the triangle XYZ and find its area given by: $\text{A}=\dfrac{1}{2}\times XY\times YZ$. Also, consider ‘XZ’ as the base and ‘YW’ as the height of the triangle XYZ and find its area given by: $\text{A}=\dfrac{1}{2}\times ZX\times YW$. Substitute all the given values of sides and equate the two areas with each other to find the value of ‘h’.
Complete step-by-step answer:
We know that, area of a triangle is given as: $\text{A}=\dfrac{1}{2}\times \text{base}\times \text{height}$, where ‘A’ is the area of the triangle.
From the given figure, we can clearly see that triangle XYZ is a right angle triangle. Therefore, considering ‘XY’ as the base and ‘ZY’ as the height of the triangle, we have,
$\text{A}=\dfrac{1}{2}\times XY\times YZ$
Substituting, XY = 6 m and YZ = 8 m, we get,
$\begin{align}
& \text{A}=\dfrac{1}{2}\times 6\times 8 \\
& \Rightarrow \text{A}=\dfrac{48}{2} \\
& \Rightarrow \text{A}=24\text{ }{{\text{m}}^{2}}..................(i) \\
\end{align}$
Now, we can also find the area of the triangle XYZ by considering ‘XZ’ as the base and ‘YW’ as the height of the triangle. Therefore,
$\text{A}=\dfrac{1}{2}\times ZX\times YW$
Substituting, XZ = 10 m and YW = h, we get,
$\begin{align}
& \text{A}=\dfrac{1}{2}\times 10\times h \\
& \Rightarrow \text{A}=5h..................(ii) \\
\end{align}$
Since, equation (i) and equation (ii) represent the area of the same triangle XYZ, therefore, the area given by these two equations must be equal.
Equating the areas given by equation (i) and equation (ii), we get,
$\begin{align}
& 24=5h \\
& \Rightarrow h=\dfrac{24}{5} \\
& \Rightarrow h=4.8\text{ m} \\
\end{align}$
Hence, option (a) is the correct answer.
Note: One may note that we can also find the area of the triangle XYZ by using heron’s formula because all the three sides have been provided to us, but this will be a lengthy process. So, to solve this question in less time and to get rid of calculation, we have applied the formula: $\text{A}=\dfrac{1}{2}\times \text{base}\times \text{height}$. You may note that the areas are equated because we are finding the area of the same triangle two different times. Never use Pythagoras theorem in the triangles XYW or ZYW to solve this problem because we do not know the length of all the sides in these triangles.
Complete step-by-step answer:
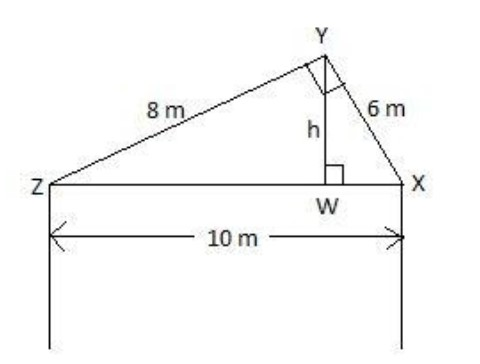
We know that, area of a triangle is given as: $\text{A}=\dfrac{1}{2}\times \text{base}\times \text{height}$, where ‘A’ is the area of the triangle.

From the given figure, we can clearly see that triangle XYZ is a right angle triangle. Therefore, considering ‘XY’ as the base and ‘ZY’ as the height of the triangle, we have,
$\text{A}=\dfrac{1}{2}\times XY\times YZ$
Substituting, XY = 6 m and YZ = 8 m, we get,
$\begin{align}
& \text{A}=\dfrac{1}{2}\times 6\times 8 \\
& \Rightarrow \text{A}=\dfrac{48}{2} \\
& \Rightarrow \text{A}=24\text{ }{{\text{m}}^{2}}..................(i) \\
\end{align}$
Now, we can also find the area of the triangle XYZ by considering ‘XZ’ as the base and ‘YW’ as the height of the triangle. Therefore,
$\text{A}=\dfrac{1}{2}\times ZX\times YW$
Substituting, XZ = 10 m and YW = h, we get,
$\begin{align}
& \text{A}=\dfrac{1}{2}\times 10\times h \\
& \Rightarrow \text{A}=5h..................(ii) \\
\end{align}$
Since, equation (i) and equation (ii) represent the area of the same triangle XYZ, therefore, the area given by these two equations must be equal.
Equating the areas given by equation (i) and equation (ii), we get,
$\begin{align}
& 24=5h \\
& \Rightarrow h=\dfrac{24}{5} \\
& \Rightarrow h=4.8\text{ m} \\
\end{align}$
Hence, option (a) is the correct answer.
Note: One may note that we can also find the area of the triangle XYZ by using heron’s formula because all the three sides have been provided to us, but this will be a lengthy process. So, to solve this question in less time and to get rid of calculation, we have applied the formula: $\text{A}=\dfrac{1}{2}\times \text{base}\times \text{height}$. You may note that the areas are equated because we are finding the area of the same triangle two different times. Never use Pythagoras theorem in the triangles XYW or ZYW to solve this problem because we do not know the length of all the sides in these triangles.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Draw a diagram of nephron and explain its structur class 11 biology CBSE

Explain zero factorial class 11 maths CBSE

Chemical formula of Bleaching powder is A Ca2OCl2 B class 11 chemistry CBSE

Name the part of the brain responsible for the precision class 11 biology CBSE

The growth of tendril in pea plants is due to AEffect class 11 biology CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




