Question

A rod of length of 2l is moving such that its end A and B move in contact with the horizontal floor and the vertical wall as shown in the figure. O is the intersection point of the vertical wall and the horizontal floor. The velocity vector of the centre of the rod C is always directed along tangent drawn at C to the:

a) circle of radius l/2 whose centre lies at O.
b) circle of radius l whose centre lies at O
c) circle of radius 2l whose centre lies at O
d) none of these

Answer 1

Hint: To determine how the velocity vector of the centre C is directed we have obtained its coordinates with respect to the centre O. Then we will see how the x and the y coordinate vary with respect to each other. Once we obtain the required relation we will be able to see how the velocity vector is given by the tangent to C with respect to the centre O.
Formula used:
Let a point P(x,y) lie on the circle with centre placed at origin and of radius R. Than the equation of the circle is given by
${{x}^{2}}+{{y}^{2}}={{R}^{2}}$.

Complete answer:

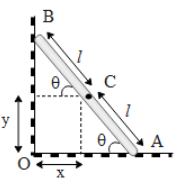
In the above diagram we can see that the rod makes an angle $\theta $with the horizontal floor. Let the centre have the coordinates (x,y) with O as the origin. Therefore from the above diagram,
$x=lCos\theta \text{, and y=}l\text{Sin}\theta $
After squaring x and y we get,
${{x}^{2}}={{l}^{2}}Co{{s}^{2}}\theta ...(1)$ and ${{y}^{2}}={{l}^{2}}Si{{n}^{2}}\theta ...(2)$
Adding equation 1 and 2 we obtain,
$\begin{align}
  & {{x}^{2}}+{{y}^{2}}={{l}^{2}}Co{{s}^{2}}\theta +{{l}^{2}}Si{{n}^{2}}\theta \\
 & {{x}^{2}}+{{y}^{2}}={{l}^{2}}(Co{{s}^{2}}\theta +Si{{n}^{2}}\theta )\text{, }\because Co{{s}^{2}}\theta +Si{{n}^{2}}\theta =1 \\
 & {{x}^{2}}+{{y}^{2}}={{l}^{2}} \\
\end{align}$
The above equation we obtained represents the equation of the circle with radius $l$. We have taken the point O as our centre of the circle. Therefore we can conclude that the velocity vector will always be tangent to the circle of radius $l$ and centre as O.

Hence the correct answer of the above question is option b.

Note:
The sine of an angle is defined as the ratio of its opposite side to that of the hypotenuse of the triangle. Similarly, the cos of an angle is defined as the ratio of its adjacent side to that of the hypotenuse of the triangle. Hence, from the above figure we defined the coordinates x and y respectively.