Question

A rod of length $1\,m$ and mass $0.5\,kg$ hinged at one end, is initially hanging vertical.The other end is now raised slowly until it makes an angle \[60^\circ \] with the vertical. The required work is: ( use \[\;g = 10{\text{ }}m{s^{ - 2}}\]).

Answer 1

Hint: in order to solve the question, we will first of all we will find the center of mass of raised rod with help of original rod using trigonometry after then we will find the difference between both the center of mass and after finding net height we will apply the formula of work done with relation of potential energy to find the work done as asked in question.

Formula used:
Work done formula
${\text{W = change in potential energy}}$
$W = mgh$
Here, $W$ = work done, $m$= mass and $g$ = gravitational constant.
$\cos \theta = \dfrac{B}{H}$
Here, $B$ refers to base and $H$ refers to hypotenuse.

Complete step by step answer:
In the question we are given a rod which is hinged at one end and the rod was initially hanging vertical. The other end is now raised slowly until it makes an angle \[60^\circ \] with the vertical and we have to find the work done.

Given, Rod of length = 1m, Mass of rod = 0.5 kg and Angle with the vertical = \[60^\circ \].

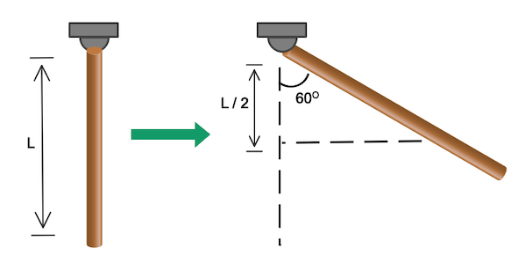
As we can see that in diagram,
center of mass of original rod = $\dfrac{L}{2}$
Now to solve the question we have to find the center of mass of rod raised at the angle we will use trigonometric formula
$\cos \theta = \dfrac{B}{H}$
Let the center of mass of raised rod be h
$B = \dfrac{L}{2}$
Therefore, Substituting the values in the formula we get
$h = \dfrac{L}{2}\cos \theta $

Now we have to find the difference of center of mass of both center of rod original and raised. Let the difference be $\Delta {\text{ }}h$.
$\Delta {\text{ }}h = \dfrac{L}{2} - \dfrac{L}{2}\cos \theta $
Taking $\dfrac{L}{2}$ common we get
$\Delta {\text{ }}h = \dfrac{L}{2}(1 - \cos \theta )$
Substituting the value of $\cos \theta $ , $\theta = 60^\circ $ so $\cos 60^\circ = \dfrac{1}{2}$
$\Delta {\text{ }}h = \dfrac{L}{2}\left( {1 - \dfrac{1}{2}} \right)$
Hence values of difference of center of masses
$\Delta {\text{ }}h = \dfrac{L}{4}$
Now we will apply the formula of work done
$W = m \times g \times \Delta {\text{ }}h$
Substituting the values of variables
$\therefore W = 0.5 \times 10 \times \dfrac{1}{4}$

Hence work done is $1.25{\text{ J}}$.

Note: Many of the students will make the mistake by solving the question using the original formula which is relation of work done with force and distance but this way of solving is incorrect as this question involves change in height so the relation of work done with change in potential energy with the help of center of mass is easy and correct way.