Question

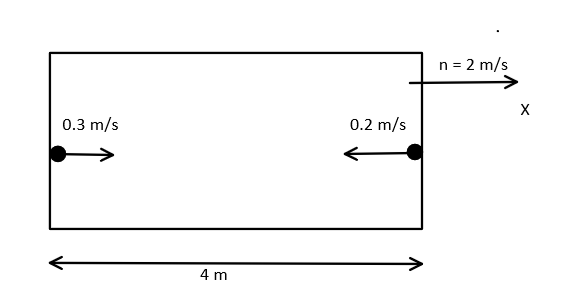
A rocket is moving in a gravity free space with a constant acceleration of $2\,m{s^{ - 2}}$ along $ + x$ direction (see figure). The length of a chamber inside the rocket is $4m$. A ball is thrown from the left end of the chamber in $ + x$ direction with a speed of $0.3\,m{s^{ - 1}}$ relative to the rocket. At the same time, another ball is thrown in $ - x$ direction with a speed of $0.2\,m{s^{ - 1}}$ from its right end relative to the rocket. The time in seconds when the two balls hit each other is:

Answer 1

Hint: This question is from the topic relative motion and we can approach the solution to this question by considering relative motion of the balls and then summing up the distances both travelled to $4m$, since this is the total distance between the two balls.

Complete step-by-step solution:
We will approach the solution to this question exactly like we explained in the hint section.
First, let’s have a look at what is given to us in the question and how we can use it to reach the answer:
Rocket has the acceleration in the right direction. Using this, we can say that acceleration of the right ball with respect to the left ball is $2\,m{s^{ - 1}}$ and the acceleration of the left ball with respect to the right ball is $ - 2\,m{s^{ - 1}}$. This information is very essential in the process of finding the answer to the question.
Now, we will consider that the distance that the right ball travelled is $S\,m$, and the distance that the left ball travelled is $\left( {4 - S} \right)\,m$ because the length of the rocket is only $4m$ .
To solve this question, we will need to use the equation of accelerated motion, which is:
$S\, = \,ut\, + \,\dfrac{1}{2}a{t^2}$
Where, $u$ is the initial velocity
$a$ is the acceleration and,
$t$ is the time taken.
For the right ball, the equation can be written as:
$S\, = \,\left( {0.3} \right)t\, + \,\dfrac{1}{2}\left( { - 2} \right){t^2}$
On the other hand, for the left ball, we get the equation as:
$4\, - \,S\, = \,\left( {0.2} \right)t\, + \,\dfrac{1}{2}\left( 2 \right){t^2}$
After substituting the value of $S$ from one equation of the other, we can find the value of time, $t$, easily as:
$t\, = \,8\,s$
Hence, the correct answer is $t\, = \,8\,s$.

Note:- Many students mistake the solution as not considering the right relative acceleration of the balls. Many times, students do not realize how immensely important the length of the rocket is in such types of questions as this enables us to find a relation so that we can find the value of time.