Question

A rocket is fired vertically up from the ground with an acceleration of $10m/{{s}^{2}}$. If its fuel is finished after 1 minute then calculate-
(a) Maximum velocity attained by rocket in ascending motion.
(b) Height attained by rocket before fuel is finished.
(c) Time taken by the rocket in the whole motion.
(d) Maximum height attained by rocket.

Answer 1

Hint: Firstly you could draw a rough diagram representing the whole motion. Then you could use Newton’s equations of motion accordingly to solve the given questions. Also remember that the initial velocity when fired as well as the velocity at maximum height is zero for the rocket.

Formula Used:
Newton’s equations of motion,
$v=u+at$
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
${{v}^{2}}-{{u}^{2}}=2as$

Complete step by step answer:
In the question, we have a rocket that is fired vertically upward with an acceleration of $10m{{s}^{-2}}$ and this rocket runs out of fuel after 1 minute. Even after completion of the fuel, we know that, due to inertia the rocket travels a short distance upward to reach a maximum height. So the situation can be represented as,

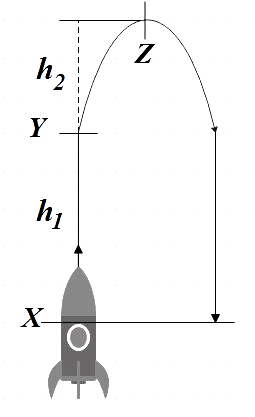
(a) Maximum velocity attained by rocket in ascending motion.
We know that initial velocity is zero when the rocket is fired. So,
$u=0$
From Newton’s equations of motion we have,
$v=u+at$ ………………… (1)
Where, v is the final velocity, ‘u’ is the initial velocity, ‘a’ is the acceleration and t is the time taken.
We are told that the rocket runs out of fuel in 1minute and we have to find the maximum velocity attained during that time interval. So,
${{t}_{Y}}=1\min =60s$
Also, acceleration is given as,
$a=10m{{s}^{-2}}$
Now (1) becomes,
${{v}_{y}}=0+\left( 10 \right)\left( 60 \right)=600m{{s}^{-1}}$
(b) Height attained by rocket before fuel is finished
In the figure Y is point where the rocket runs out of fuel, so we are to find the distance from X to Y, that is, ${{h}_{1}}$
From Newton’s equations,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$ ……………………………. (2)
$\Rightarrow {{h}_{1}}=0+\dfrac{1}{2}\times 10\times {{\left( 60 \right)}^{2}}$
$\Rightarrow {{h}_{1}}=18000m=18km$
(d) Maximum height attained by rocket.
Let us find${{h}_{2}}$. At point Y the rocket has maximum velocity ${{v}_{y}}$ and at point Z, that is, at the maximum height the velocity is zero.
From Newton’s equations,
${{v}^{2}}-{{u}^{2}}=2as$
$\Rightarrow {{0}^{2}}-{{v}_{y}}^{2}=-2g{{h}_{2}}$
$\Rightarrow {{h}_{2}}=\dfrac{{{\left( 600m{{s}^{-1}} \right)}^{2}}}{2\times 10m{{s}^{-2}}}=18000m=18km$
Maximum height reached by rocket is the distance from X to Z,
$\Rightarrow {{H}_{\max }}={{h}_{1}}+{{h}_{2}}=18km+18km$
$\Rightarrow {{H}_{\max }}=36km$
(c) Time taken by the rocket in the whole motion.
Time taken to travel from Y to Z can be given by,
From (1),
$0={{v}_{y}}-gt$
${{t}_{Y\to Z}}=\dfrac{{{v}_{y}}}{g}=\dfrac{600}{10}=60s$
Time taken for the return journey,
From (2),
${{H}_{\max }}=0+\dfrac{1}{2}g{{t}_{r}}^{2}$
${{t}_{r}}^{2}=\dfrac{2{{H}_{\max }}}{10}=\dfrac{2\times 36000}{10}$
${{t}_{r}}=60\sqrt{2}s$
The total time taken by rocket for whole motion T is,
$T={{t}_{Y}}+{{t}_{y\to z}}+{{t}_{r}}$
$\Rightarrow T=\left( 60+60+60\sqrt{2} \right)s$
$\Rightarrow T=60\left( 2+\sqrt{2} \right)s$
$\Rightarrow T=\left( 2+\sqrt{2} \right)\min $

So we have the solutions as,
(a) Maximum velocity attained by rocket in ascending motion is $600m{{s}^{-1}}$
(b) Height attained by rocket before fuel is finished $18km$
(c) Time taken by the rocket in the whole motion $\left( 2+\sqrt{2} \right)\min $
(d) Maximum height attained by rocket $36km$

Note:
After the fuel is used up, the acceleration of the rocket is that due to gravity (g). But we have to be careful about the direction as by convention we take g as positive downward. Hence, we have taken g as positive while calculating the time taken for return journey and we have taken g as negative while calculating ${{h}_{2}}$ and ${{t}_{Y\to Z}}$.