Question

A river 800m wide flows at the rate of $5km{h^{ - 1}}$ . A swimmer who can swim at $10km{h^{ - 1}}$ in still water, wishes to cross the river straight.
(i) Along what direction must he strike?
(ii) What should be his resultant velocity?
(iii) How much time he would take?

Answer 1

Hint: The swimmer has to start at some angle in the direction opposite to the flow of the river. The speed of the rotation of the object in relation to another object is referred to as angular velocity. The swimmer has to move opposite the flow of the velocity.

Complete step by step answer:
Following is the diagram representing the situation given in the question.

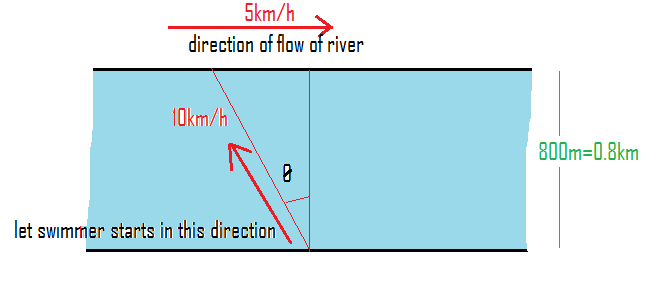
(i) According to the question the swimmer wants to cross the river straight.
So let $\theta$ be the angle with which the swimmer should start in order to cross the river straight.
Let us write the tangent of the angle using the above diagram.
$\tan \theta = \dfrac{{5km/h}}{{10km/h}} = \dfrac{1}{2}$
Let us write the angle for which tan gives $\dfrac{1}{2}$
$\theta = {\tan ^{ - 1}}\dfrac{1}{2} = {30^o}$
So, the swimmer must start at an angle $30^{\circ}$ to cross the river straight.

(ii) If we resolve the velocity of the swimmer in its components, then the component along the motion is shown in the figure below.

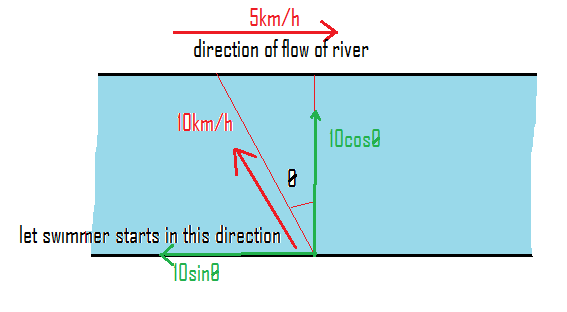
${V_{\text{resultant}}} = 10\cos \theta $
Now let us substitute the value of $\theta$.
${V_{\text{resultant}}} = 10\cos 30 = 10 \times \dfrac{{\sqrt 3 }}{2}$
Let us further simplify it.
${V_{\text{resultant}}} = 5\sqrt 3 = 8.66km/h$
Hence, the resultant velocity is 8.66km/h.

(iii) Let $t$ is the time taken by the swimmer to cross the river.
Let us use the formula speed = distance/time and the width of the river is 800m (given).
So time taken by the swimmer is calculated as below.
$t = \dfrac{{0.8km}}{{8.66km/h}}$
Let us further simplify it.
$t = 0.0924hr = 5.54\min = 332.56\sec $

$\therefore $(i) The swimmer must strike at an angle $30^{\circ}$ to cross the river straight.
(ii) His resultant velocity is $8.66 kmph$.
(iii) He would take $332.56$ seconds to cross the river.

Note:
The horizontal component of swimmers' velocity will work on the velocity of river flow.
Only the vertical component of swimmers' velocity will contribute to helping him to cross the river.
The basic formula is always going to be used in this type of problem if speed = distance/time.