Question

A right triangle has angles which measure 30, 60 and 90 degrees. If the perimeter of this triangle is \[15 + 5\sqrt 3 \] then what is the length of the hypotenuse of this triangle. \[\]

Answer 1

Hint:

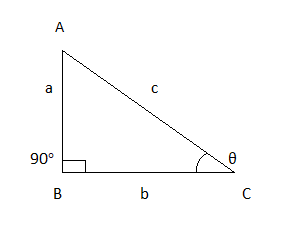
 Let the right angle triangle is $\Delta ABC$ where,
\[
  \angle ABC = 90^\circ \\
  \angle ACB = \theta \\
 \]
AB = opposite side of the angle \[\angle ACB = \theta \] = a
BC = Adjacent side of the angle \[\angle ACB = \theta \] = b
CA= Hypotenuse of the triangle = c
Sine, Cosine and Tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle:
\[\sin \theta = \dfrac{{{\text{opposite}}}}{{{\text{Hypotenuse}}}} = \dfrac{a}{c}\]
\[\cos \theta = \dfrac{{{\text{adjacent}}}}{{{\text{Hypotenuse}}}} = \dfrac{b}{c}\]
\[\tan \theta = \dfrac{{{\text{opposite}}}}{{{\text{Adjacent}}}} = \dfrac{a}{b}\]
Using these formulas we will find the values of “a” and “b” and substitute it in the formula of perimeter so that the value of hypotenuse is found from it.

Complete step by step answer:
It is given that the A right triangle has angles which measure 30, 60 and 90 degrees.

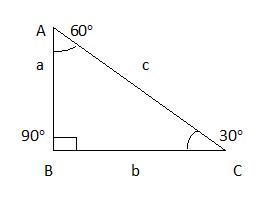
Let the right angle triangle is ∆ABC where,
\[
  \angle ABC = 90^\circ \\
  \angle ACB = 30^\circ \\
  \angle CAB = 60^\circ \\
 \]
AB = opposite side of the angle \[\angle ACB\] = a
That is AB is the opposite side of the angle 30° which is denoted as “a”
BC = Adjacent side of the angle \[\angle ACB\] = b
That is BC is the adjacent side of the angle 30° which is denoted as “b”
CA is hypotenuse of the triangle which is denoted as “c”
We need to find out the value of c.
From $\Delta ABC$ we get,
Applying the sine and cosine as ratio of sides of a right angled triangle we have the following,
\[
  \sin 30^\circ = \dfrac{{{\text{opposite}}}}{{{\text{Hypotenuse}}}} = \dfrac{a}{c} \\
  \dfrac{a}{c} = \sin 30^\circ = \dfrac{1}{2} \\
 \]
\[
  \cos 30^\circ = \dfrac{{{\text{adjacent}}}}{{{\text{Hypotenuse}}}} = \dfrac{b}{c} \\
  \dfrac{b}{c} = \cos 30^\circ = \dfrac{{\sqrt 3 }}{2} \\
 \]
Now it is given that the perimeter of this triangle is \[15 + 5\sqrt 3 \].
We know the formula of perimeter of a triangle is \[a + b + c\],
Therefore we get, \[a + b + c = 15 + 5\sqrt 3 \]
Let us divide both sides of the above equation by “c” we get,
\[\dfrac{{a + b + c}}{c} = \dfrac{{15 + 5\sqrt 3 }}{c}\]
Here let us split the division therefore we get,
\[\dfrac{a}{c} + \dfrac{b}{c} + \dfrac{c}{c} = \dfrac{{15 + 5\sqrt 3 }}{c}\]
Let us substitute the values we have got,
\[\dfrac{1}{2} + \dfrac{{\sqrt 3 }}{2} + 1 = \dfrac{{15 + 5\sqrt 3 }}{c}\]
On simplifying the above equation we get,
\[\dfrac{{15 + 5\sqrt 3 }}{c} = \dfrac{3}{2} + \dfrac{{\sqrt 3 }}{2}\]
Let us cross multiply to get the value of c,
\[(3 + \sqrt 3 )c = 2(15 + 5\sqrt 3 )\]
On further solving we get,
\[c = \dfrac{{2 \times 5(3 + \sqrt 3 )}}{{3 + \sqrt 3 }}\]
Let us cancel out the same terms in the numerator and denominator, we get
\[c = 10\]
Hence, the length of the hypotenuse of this triangle is 10 units.

Note:
We have used the value of the $\sin $ and $\cos $ function at ${30^ \circ }$
$\sin ({30^ \circ }) = $\[\dfrac{1}{2}\] and $\cos ({30^ \circ }) = $\[\dfrac{{\sqrt 3 }}{2}\] .The exact value of cos 30 degrees is written as 0.8660 approx and the exact value of sin 30 degrees is 0.5.