Question

A right circular cone has a height of 9cms and radius of the base 5cms. It is inverted and water is poured into it. If at any instant the water level rises at a rate of \[\left( \dfrac{\pi }{A} \right)\] cms/sec., where ‘A’ is the area of water surface at that instant, show that the vessel will be full in 75 seconds.

Answer 1

Hint: Given that the parameter changing is the height of the cone, frame a relation between the height of the cone and radius of the cone. For that, consider at some instant the height and radius of the cone as ‘h’ and ‘r’ respectively. Then we can use similar triangles conditions to obtain the required relation from total height and radius. After differentiating with respect to time and substitute given information and integrate with limits as follows
Time changes from 0 to T where T = time required to full the vessel
And height changes from 0 to H where H = total height of the vessel.

Complete step by step answer:
Now, let us consider that
Height of vessel, H = 9cm
The radius of base of the vessel, R = 5cm
Rate of change of height, \[\dfrac{dh}{dt}\] = \[\dfrac{\pi }{A}\]cm/s
Considering that at some instant of time the water is at height ‘h’ having radius ‘r’ as shown in the figure below.

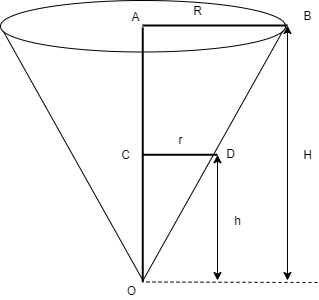
In the above figure, since all the angles in the triangle \[\Delta OAB\]and \[\Delta OCD\]are equal we can say that \[\Delta OAB\] is similar to\[\Delta OCD\].
So, from the similarity condition we can take
 \[\Rightarrow \dfrac{OA}{OC}=\dfrac{AB}{CD}\]
\[\Rightarrow \dfrac{H}{h}=\dfrac{R}{r}\]
\[\Rightarrow h=\dfrac{H}{R}.r\]
Now differentiating with respect to time (t) on both sides we get
\[\begin{align}
  & \Rightarrow \dfrac{dh}{dt}=\dfrac{H}{R}.\dfrac{dr}{dt} \\
 & \\
\end{align}\]
Substituting, \[\dfrac{dh}{dt}=\dfrac{\pi }{A}\] where \[A=\pi {{r}^{2}}\] at that instant we get
\[\begin{align}
  & \Rightarrow \dfrac{\pi }{\pi {{r}^{2}}}=\dfrac{H}{R}.\dfrac{dr}{dt} \\
 & \\
\end{align}\]
Bringing ‘r’ terms one side and ‘t’ terms one side we get
\[\Rightarrow dt=\dfrac{H}{R}.{{r}^{2}}dr\]
Suppose vessel will be full in time ‘T’
Now at t=0, r=0 and at t=T, r=R
So, integrating on both sides by applying limits we get
\[\begin{align}
  & \Rightarrow \int\limits_{0}^{T}{dt}=\dfrac{H}{R}\int\limits_{0}^{R}{{{r}^{2}}dr} \\
 & \Rightarrow \left[ t \right]_{0}^{T}=\dfrac{H}{R}\left[ \dfrac{{{r}^{3}}}{3} \right]_{0}^{R} \\
 & \Rightarrow T-0=\dfrac{H}{R}\left[ \dfrac{{{R}^{3}}}{3}-\dfrac{{{0}^{3}}}{3} \right] \\
 & \Rightarrow T=\dfrac{H.{{R}^{2}}}{3} \\
\end{align}\]
Substituting H = 9 and R = 5 in above equation we get
\[\begin{align}
  & \Rightarrow T=\dfrac{{{9.5}^{2}}}{3} \\
 & \Rightarrow T=75s \\
\end{align}\]
Therefore it is proved that vessel will be full in 75 seconds.

Note:
The main part at which one can do mistakes is that while taking condition from the similarity of triangles. You need to be very careful in taking the ratio of sides correctly.
The correct ratio is
\[\Rightarrow \dfrac{OA}{OC}=\dfrac{AB}{CD}\]
Some students may take the ratio of one side inverted due to confusion.
 Also, you need to be careful how the limits of parameters change with respect to time. That is at what time the value of ‘h’ changes need to be taken care.