Question

A right circular cone has a given curved surface A. Show that when it’s volume is maximum the ratio of the height to the base radius is $\sqrt{2}:1$ ?

Answer 1

Hint: Try to find the height ‘h’ of cone in terms of Area $A=\pi rl$(by putting $l=\sqrt{{{r}^{2}}+{{h}^{2}}}$). Put the value of ‘h’ in volume expression $V=\dfrac{1}{3}\pi {{r}^{2}}h$ and differentiate w.r.t ‘r’ equating to 0. Then simplify to obtain the required proof.

Complete step-by-step answer:
As we know, the formula for the curved surface area of a cone which does not include the area of the base is $A=\pi rl$, where ‘r’ is the radius of the base and ‘l’ is the lateral height (slant height)

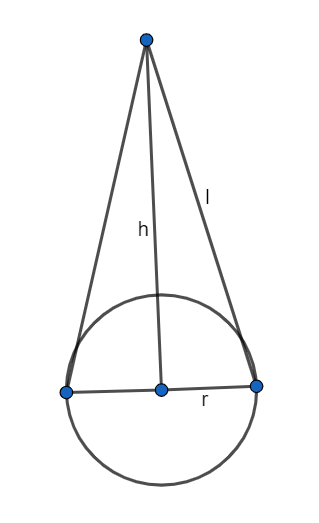
Pythagoras' theorem: If we have a right angle triangle with height ‘a’, base ‘b’ and hypotenuse ‘c’ then
$c=\sqrt{{{a}^{2}}+{{b}^{2}}}$
Using Pythagoras' theorem for the above figure, we get
$l=\sqrt{{{r}^{2}}+{{h}^{2}}}$
Substituting the value of ‘l’ in $A=\pi rl$, we get
$\begin{align}
  & A=\pi r\sqrt{{{r}^{2}}+{{h}^{2}}} \\
 & \Rightarrow {{A}^{2}}={{\pi }^{2}}{{r}^{2}}\left( {{r}^{2}}+{{h}^{2}} \right) \\
 & \Rightarrow {{A}^{2}}={{\pi }^{2}}{{r}^{4}}+{{\pi }^{2}}{{r}^{2}}{{h}^{2}} \\
 & \Rightarrow {{\pi }^{2}}{{r}^{2}}{{h}^{2}}={{A}^{2}}-{{\pi }^{2}}{{r}^{4}} \\
 & \Rightarrow {{h}^{2}}=\dfrac{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}}{{{\pi }^{2}}{{r}^{2}}} \\
 & \Rightarrow h=\dfrac{\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}}}{\pi r} \\
\end{align}$
Again we know the volume $V=\dfrac{1}{3}\pi {{r}^{2}}h$
Substituting the value of ‘h’, we get
$\begin{align}
  & V=\dfrac{1}{3}\pi {{r}^{2}}\dfrac{\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}}}{\pi r} \\
 & \Rightarrow V=\dfrac{1}{3}r\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}} \\
 & \Rightarrow V=\dfrac{1}{3}r{{\left( {{A}^{2}}-{{\pi }^{2}}{{r}^{4}} \right)}^{\dfrac{1}{2}}} \\
\end{align}$
Taking derivative w.r.t ‘r’, we get
\[\begin{align}
  & \dfrac{dV}{dr}=\dfrac{d}{dr}\left( \dfrac{1}{3}r{{\left( {{A}^{2}}-{{\pi }^{2}}{{r}^{4}} \right)}^{\dfrac{1}{2}}} \right) \\
 & \Rightarrow \dfrac{dV}{dr}=\dfrac{1}{3}\left[ r\left( \dfrac{1}{2} \right){{\left( {{A}^{2}}-{{\pi }^{2}}{{r}^{4}} \right)}^{-\dfrac{1}{2}}}\left( -4{{\pi }^{2}}{{r}^{3}} \right)+{{\left( {{A}^{2}}-{{\pi }^{2}}{{r}^{4}} \right)}^{\dfrac{1}{2}}} \right] \\
 & \Rightarrow \dfrac{dV}{dr}=\dfrac{1}{3}\left( \dfrac{-2{{\pi }^{2}}{{r}^{4}}}{\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}}}+\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}} \right) \\
 & \Rightarrow \dfrac{dV}{dr}=\dfrac{-2{{\pi }^{2}}{{r}^{4}}+{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}}{3\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}}} \\
 & \Rightarrow \dfrac{dV}{dr}=\dfrac{-3{{\pi }^{2}}{{r}^{4}}+{{A}^{2}}}{3\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}}} \\
\end{align}\]
For maximum volume,
\[\begin{align}
  & \dfrac{dV}{dr}=0 \\
 & \Rightarrow \dfrac{-3{{\pi }^{2}}{{r}^{4}}+{{A}^{2}}}{3\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}}}=0 \\
 & \Rightarrow -3{{\pi }^{2}}{{r}^{4}}+{{A}^{2}}=0 \\
 & \Rightarrow {{A}^{2}}=3{{\pi }^{2}}{{r}^{4}} \\
\end{align}\]
Substituting the value of $A=\pi r\sqrt{{{r}^{2}}+{{h}^{2}}}$, we get
${{\pi }^{2}}{{r}^{2}}\left( {{r}^{2}}+{{h}^{2}} \right)=3{{\pi }^{2}}{{r}^{4}}$
Dividing both sides by ${{\pi }^{2}}{{r}^{2}}$, we get
$\begin{align}
  & \Rightarrow \dfrac{{{\pi }^{2}}{{r}^{2}}\left( {{r}^{2}}+{{h}^{2}} \right)}{{{\pi }^{2}}{{r}^{2}}}=\dfrac{3{{\pi }^{2}}{{r}^{4}}}{{{\pi }^{2}}{{r}^{2}}} \\
 & \Rightarrow {{r}^{2}}+{{h}^{2}}=3{{r}^{2}} \\
 & \Rightarrow {{h}^{2}}=2{{r}^{2}} \\
 & \Rightarrow \dfrac{{{h}^{2}}}{{{r}^{2}}}=2 \\
 & \Rightarrow \dfrac{h}{r}=\dfrac{\sqrt{2}}{1} \\
\end{align}$
Hence Proved.

Note: Volume should be written in terms of ‘h’ which can be obtained from area. For maximum volume the first derivative of the volume function should be equal to 0 i.e. \[\dfrac{dV}{dr}=0\] and the second derivative of the volume function should be negative.
$\begin{align}
  & \dfrac{{{\partial }^{2}}V}{\partial {{r}^{2}}} \\
 & =\dfrac{d}{dr}\left( \dfrac{dV}{dr} \right) \\
 & =\dfrac{d}{dr}\left( \dfrac{-3{{\pi }^{2}}{{r}^{4}}+{{A}^{2}}}{3\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}}} \right) \\
\end{align}$
The derivative of the form $\dfrac{u}{v}=\dfrac{vdu-udv}{{{v}^{2}}}$
\[\begin{align}
  & =\dfrac{\left( 3\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}} \right)\dfrac{d}{dr}\left( -3{{\pi }^{2}}{{r}^{4}}+{{A}^{2}} \right)-\left( -3{{\pi }^{2}}{{r}^{4}}+{{A}^{2}} \right)\dfrac{d}{dr}\left( 3\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}} \right)}{{{\left( 3\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}} \right)}^{2}}} \\
 & =\dfrac{\left( 3\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}} \right)\left( -12{{\pi }^{2}}{{r}^{3}} \right)+\left( -3{{\pi }^{2}}{{r}^{4}}+{{A}^{2}} \right)\left( 12{{\pi }^{2}}{{r}^{3}}{{\left( \sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}} \right)}^{-\dfrac{1}{2}}} \right)}{{{\left( 3\sqrt{{{A}^{2}}-{{\pi }^{2}}{{r}^{4}}} \right)}^{2}}} \\
\end{align}\]
Since the numerator is the summation of two negative quantities and the denominator is a square term so we can conclude that $\dfrac{{{\partial }^{2}}V}{\partial {{r}^{2}}}$ is negative.
Hence, the maxima exists.
Now we can move forward for \[\dfrac{dV}{dr}=0\] which is already done earlier in the solution part.