Question

A right angled prism (\[{{45}^{\circ }}-{{90}^{\circ }}-{{45}^{\circ }}\]) of refractive index n has a plate of refractive index \[{{n}_{1}}\\\left( {{n}_{1}}

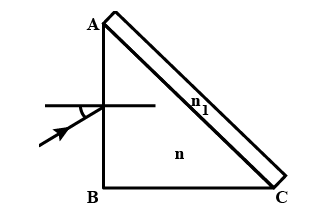
(a) Calculate the angle of incidence at AB for which the ray strikes the diagonal face at the critical angle.
(b) Assuming n=1.352, calculate the angle of incident at AB for which the refracted ray passes through the diagonal face undeviated.

Answer 1

Hint: Using Snell's law we will find the angle of incidence as we know the refractive indexes and the angle of refraction as well. Therefore, the light passing through two different isotropic media forms the Snell's law formula as:
\[n\sin x=m\sin y\]
where n is the incident index, m is the refractive index, x is the incident angle, y is the refractive angle.

Complete step by step solution:
When the light passes from AB as given below, is taken as incident light with a critical angle of c and is refracted from the inclined part of the prism at an angle 90. Hence, the value of the angle c is given as:
\[c=si{{n}^{-1}}\left( \dfrac{{{n}_{1}}}{n} \right)\ with \\left( {{n}_{1}}Now using the Snell's law on the inclined plane we take the angle of refraction as \[{{45}^{\circ }}\text{ }-\text{ }c\]degrees.
Now, the incident angle \[{{\theta }_{i}}\] of light in air is 1. Placing all these values in the formula \[i.sin{{\theta }_{i}}\text{ }=\text{ }r.\sin {{\theta }_{r}}\] for side AB, we get the value of the angle of incident as:
\[\Rightarrow 1\times sin{{\theta }_{i}}\text{ }=\text{ }r\times sin\left( 45-{{\sin }^{-1}}\dfrac{{{n}_{1}}}{n} \right)\]
\[\Rightarrow {{\theta }_{i}}\text{ }=\text{ si}{{\text{n}}^{-1}}\left( r\times sin\left( 45-{{\sin }^{-1}}\dfrac{{{n}_{1}}}{n} \right) \right)\]
(ii) Now we assume the refractive index of the diagonal plate as \[n\text{ }=\text{ }1.352\]. When the ray passes the diagonal faces and surface AB directly. The value of the refractive index incident ray is taken as 1 and the refractive angle is similar to the angle of prism which is 45 degrees due to undeviated light ray. Hence, placing all the values in the Snell's Law we get the incident ray angle as:
\[i.sin{{\theta }_{i}}\text{ }=\text{ }r.\sin {{\theta }_{r}}\] with \[{{\theta }_{r}}={{45}^{\circ }}\] and \[r=n\].
\[1.sin{{\theta }_{i}}\text{ }=\text{ }n.\sin {{45}^{\circ }}\]
\[{{\theta }_{i}}\text{ }=\text{ si}{{\text{n}}^{-1}}\left( n.\sin {{45}^{\circ }} \right)\]
\[{{\theta }_{i}}\text{ }=\text{ si}{{\text{n}}^{-1}}\left( 1.352\times \dfrac{1}{\sqrt{2}} \right)\]
Therefore, when the light ray passes the surface AB undeviated, the angle of incidence is \[\text{si}{{\text{n}}^{-1}}\left( 1.352\times \dfrac{1}{\sqrt{2}} \right)\].

Note: The critical angle is defined as the angle of incidence which when enters a certain refractive index and direction forms a certain critical value, and the reflected line lies on a straight line with an angle of refraction of 90-degrees. This phenomenon happens when the incident ray travels from denser to rarer medium.