Question

A rectangular plot is given for constructing a house having a measurement of 40m length and 15m in the front. According to the laws, a minimum of 3m wide space should be left in the front and back and 2m wide space on each of the other sides. Find the largest area where the house can be constructed.

Answer 1

Hint: For solving this question, the length of the rectangular plot is 40m and the breadth of the plot is 15 m. According to the given condition in the question, a minimum of 3 m wide space should be left in the front and back and 2 m wide space on each of the other sides. By using this condition, we can easily find the actual length and breadth of the plot. By using the formula of the area of the rectangle we can find the area of the house constructed.
Complete step-by-step answer:

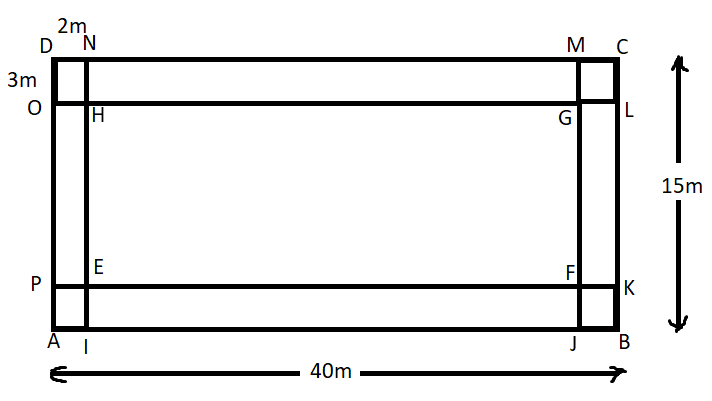
Formula used in the question is:
Area of rectangle = length $\times $ breadth.
The rectangular plot ABCD where length is 40 m and width is 15 m.
According to the given condition in the question, a minimum of 3 m wide space should be left in the front and back and 2 m wide space on each of the other sides.
$\therefore $OD = CL = AP = BK = 3m and DN = CM = BJ = AI = 2m
So, the actual length where house can be constructed
$=EH=AD-\left( DO+AP \right)=40m-\left( 3m+3m \right)=34m$
And the actual width where house can be constructed
$=EF=AB-\left( AI+BJ \right)=15m-\left( 2m+2m \right)=11m$
Area of rectangle $=length\times breadth$
Area of house constructed $=EF\times EH=34m\times 11m=374{{m}^{2}}$ .
Hence, the largest area where the house can be constructed is $374{{m}^{2}}$.
Note: Students must not directly apply the area of the rectangle to the given length and breadth. First the extra space should be provided as mentioned in the question which reduces the length and breadth and then the area of the rectangle should be applied to final dimensions for obtaining the correct answer.