Question

A rectangle is inscribed in an equilateral triangle of side length 2a units. The maximum area of this rectangle can be

a.\[\sqrt{3}{{a}^{2}}\]

b.\[\dfrac{\sqrt{3}{{a}^{2}}}{4}\]

c.\[\dfrac{\sqrt{3}{{a}^{2}}}{2}\]

d.\[{{a}^{2}}\]

Answer 1

Hint: Proceeding the question by first drawing the figure, we try to evaluate the area of the rectangle inscribed in the equilateral triangle in terms of only one variable. Then we will differentiate the obtained area to get the value of the variable at which the area is maximum.

Complete step-by-step answer:
First of all, we will draw the figure of the given question.

We draw an equilateral triangle ABC and inscribe a rectangle inside it given by DEFG, where the side D meets line AB, E meets line AC and F and G meet line BC of the equilateral triangle.

Let the length of line BC be 2a, because the given equilateral triangle is of side 2a and let the length of line FG be l then the remaining part of the line BC becomes

BF = GC = \[\dfrac{2a-l}{2}\] .
Using all these above calculations and assumptions we obtain the figure as ,

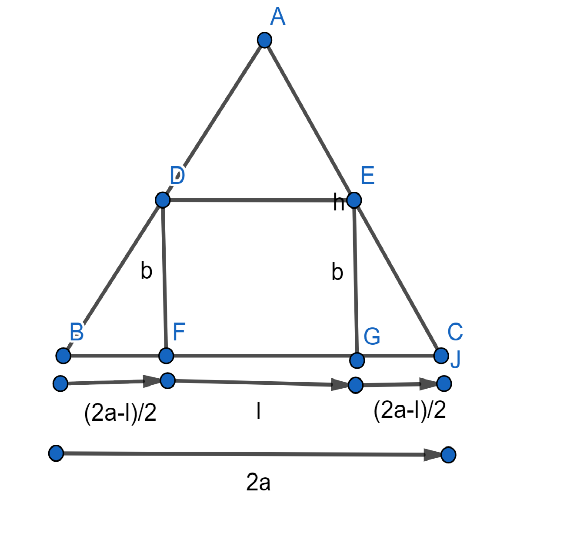
Now consider the triangle DBF,
\[\angle DBF=60\] as it comes under the angle of equilateral triangle, which have all angles as 60.

Using trigonometric properties of tan and applying tan on triangle DBF we get,
 \[\tan 60=\dfrac{b}{(2a-l)/2}\]

We have value of tan 60 = \[\sqrt{3}\] , substituting it in above we get,
\[\begin{align}
  & \sqrt{3}=\dfrac{2b}{(2a-l)} \\
 & \Rightarrow b=\dfrac{\sqrt{3}(2a-l)}{2} \\
\end{align}\]

Now as DEFG is a rectangle and area of the rectangle is lb, where l is the length and b is breadth of the rectangle.
Therefore, Area of rectangle DEFG = l×b

We earlier obtained breadth of the rectangle as
 \[b=\dfrac{\sqrt{3}(2a-l)}{2}\] .

Then the area of rectangle DEFG becomes
\[A=l\left( \dfrac{\sqrt{3}(2a-l)}{2} \right)\]
For maximum area we evaluate \[\dfrac{dA}{dl}\] and substitute \[\dfrac{dA}{dl}=0\]

We have, \[A=l\left( \dfrac{\sqrt{3}(2a-l)}{2} \right)\]
Differentiating the above with respect to l we get,

\[\dfrac{dA}{dl}=\dfrac{\sqrt{3}}{2}\left( 2a-2l \right)\]
Equating \[\dfrac{dA}{dl}=0\]we get,
\[\dfrac{dA}{dl}=\dfrac{\sqrt{3}}{2}\left( 2a-2l \right)=0\]

\[\Rightarrow 2a-2l=0\]

\[\Rightarrow a=l\]

Therefore, Maximum Area = l×b will be obtained by substituting a=l in area A and breadth b.

Hence, maximum area is

\[A=a\dfrac{\sqrt{3}}{2}\left( 2a-a \right)\]
\[\Rightarrow A=\dfrac{\sqrt{3}}{2}{{a}^{2}}\]
Hence, we have Maximum Area \[A=\dfrac{\sqrt{3}}{2}{{a}^{2}}\] ​, which is option (c).


Note: The possibility of error in the question is at the point where we try to calculate the area of the rectangle inscribed in the equilateral triangle. Always try to obtain area in one single variable rather than going for multiple variables. This helps while differentiating it as then we do not have to rely only on one variable used in an area.