Question

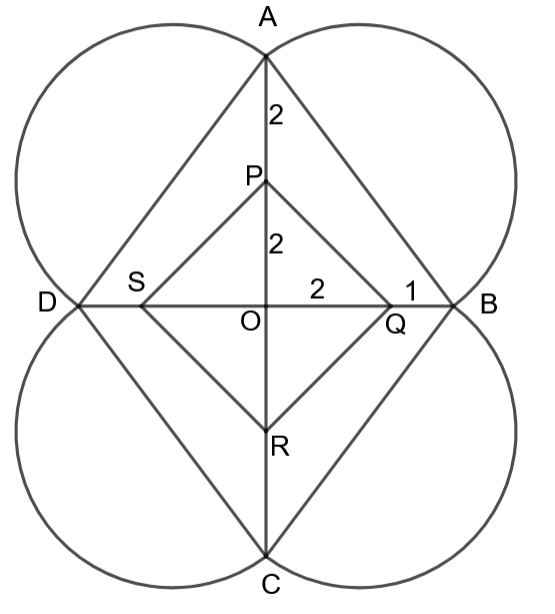
A rangoli has been drawn on a floor of a house. ABCD and PQRS both are in the shape of a rhombus. Find the radius of the semicircle drawn on each side of the rhombus ABCD.

Answer 1

Hint: To solve this question, we should know the properties of the rhombus and the Pythagoras theorem of a right angled triangle. We know that in a rhombus ABCD, the diagonals AC and BD bisect each other and they are at an angle of ${{90}^{\circ }}$. In a right angled triangle with the lengths of the sides as $a,b,c$ where $c$ is the hypotenuse, the relation between $a,b,c$ can be written as ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$. Using the above properties, we can find the length of the side AB. From the diagram, we can infer that the side AB is the diameter of the semicircle. So, we can find the radius of the circle by the relation $\text{radius}=\dfrac{\text{diameter}}{2}$.

Complete step-by-step answer:

In the given question, we have two rhombuses ABCD and PQRS. We are asked to find the radius of the semicircle drawn on each side of the rhombus. Let us consider the rhombus ABCD.
The lines AC and BD are the diagonals of ABCD. From the diagram given in the question, we can infer that the point O is the point of intersection of the diagonals of the rhombus ABCD. We know the property of the rhombus which is the diagonals of a rhombus bisect each other and the angle between the diagonals is always ${{90}^{\circ }}$. In the diagram given in the question, the lengths of the sides can be written as
$\begin{align}
  & AO=AP+PO=2+2=4 \\
 & OB=OQ+QB=2+1=3 \\
\end{align}$
 Using the diagonals property, we can write that
$\begin{align}
  & AO=OC=4 \\
 & BO=OD=3 \\
 & \angle AOB={{90}^{\circ }} \\
\end{align}$
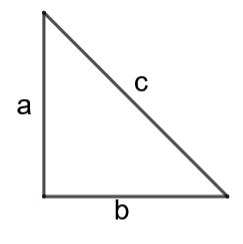
Let us consider the triangle $\Delta AOB$. As the angle $\angle AOB={{90}^{\circ }}$, we can infer that the triangle is a right angled triangle. The side AB is the hypotenuse.
In a right angled triangle with the lengths of the sides as $a,b,c$ where $c$ is the hypotenuse, the relation between $a,b,c$ can be written as ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$.

Using this relation, we get
$A{{O}^{2}}+O{{B}^{2}}=A{{B}^{2}}$
Substituting the values of AO and OB, we get
$\begin{align}
  & {{4}^{2}}+{{3}^{2}}=A{{B}^{2}} \\
 & A{{B}^{2}}=16+9=25 \\
 & AB=\sqrt{25}=5 \\
\end{align}$
We know that all the sides of a rhombus are equal. So, we can write that
$AB=BC=CD=DA$
We can infer from the question that the arcs drawn are the semicircles which mean that the chord joining the end points will be its diameter. So, the sides of the rhombus ABCD are the diameters of the semicircles which are attached to them. We know that the relation between the diameter and radius of a circle as
$\text{radius}=\dfrac{\text{diameter}}{2}$.
So, we can write the radii of the semicircles as
$\text{radius}=\dfrac{\text{AB}}{2}=\dfrac{5}{2}=2.5\text{ units}$
$\therefore $ The required radius of the semicircles is 2.5 units.

Note: The important point to remember about the properties of the rhombus is that the sides are equal and the diagonals bisect each other. Some students, forgetting these properties, might interpret the question as to find the lengths of the sides AB, BC, CD, DA separately and try to find them with repeated calculations. They might also think that the values of OC, OD should also be given and they think that the question has insufficient information.