Question

A railway track is banked for a speed v, by making the height of the outer rail h higher than that of the inner rail. The distance between the rails is d. The radius of curvature of the track is r. Then,
$\begin{align}
  & a)\dfrac{h}{d}=\dfrac{{{v}^{2}}}{rg} \\
 & b)\tan ({{\sin }^{-1}}\dfrac{h}{d})=\dfrac{{{v}^{2}}}{rg} \\
 & c){{\tan }^{-1}}\dfrac{h}{d}=\dfrac{{{v}^{2}}}{rg} \\
 & d)\dfrac{h}{r}=\dfrac{{{v}^{2}}}{dg} \\
\end{align}$

Answer 1

Hint: The above given options are the conditions which are required to be satisfied such that the train on the banking does not fall. Given h is the maximum height till which the track can be banked or else the train will fall towards the inside of the track. Hence by drawing the free body diagram of the train on the bank such that there is no unbalanced force will give us the required condition from the options provided.

Complete step-by-step answer:

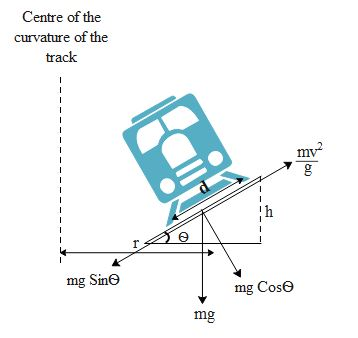
When the train moves on a banked track it has a tendency of falling towards the inner side of the circular track. Hence the train has to move some velocity. When the train moves with some velocity it experiences a radially outward force. This force prevents the train from falling due to the component of the gravitational force. The train will move steadily if there is no unbalanced force acting on it i.e. the net force on the train is zero. If we see the above figure the component of gravity i.e. $mg\operatorname{cos}\theta $ is cancelled by the normal force to the ground. The component of gravity i.e. $mgsin\theta $ is cancelled by the radially outward force. Mathematically this is written as,
$mgS in\theta =\dfrac{m{{v}^{2}}}{r}$
where v is the velocity of the train and r is the radius of curvature of the track.

From the above diagram, $\operatorname{sin}\theta =\dfrac{Opp}{Hyp}=\dfrac{h}{d}$. Hence substituting this in the above equation we get,
$\begin{align}
  & \dfrac{hg}{d}=\dfrac{{{v}^{2}}}{r} \\
 & \dfrac{h}{d}=\dfrac{{{v}^{2}}}{rg} \\
\end{align}$

So, the correct answer is “Option A”.

Note: There is a possibility that the train not only falls towards the inside of the track but it may also skid away from the track. If the velocity of the train is increased to a particular extent it will overcome the component of gravity along the incline. Usually the wheels of the train are interlocked with the rails, hence we can ignore the frictional force along the incline.