Question

A race track is in the form of a ring whose inner circumference is $352$m and the outer circumference is $396$ m. The width of the track is-
A.$14$ m
B.$7$ m
C.$21$ m
D.$\dfrac{7}{2}$ m

Answer 1

Hint: First let us assume the radius of outer circumference to be R, the radius of inner circumference to be r and the width of the track to be l. Then use the formula of circumference of the circle to find the radius of inner circumference and radius of outer circumference. Then subtract the inner radius from outer radius to get the answer.

Complete step-by-step answer:
Given, a race track is in the form of a ring and the inner circumference of the ring =$352$m
The outer circumference of the ring=$396$ m
We have to find the width of the race track.

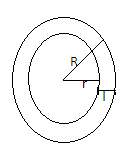
Let the radius of outer circumference be R and the radius of inner circumference be r. The width of the track is l.
Then, from the figure, we can say that width of race track (l) =R-r -- (i)
Now we know that the circumference of the inner circle is=$2\pi r$ where r is the radius of inner circumference.
On putting the given values in the above formula we get-
$ \Rightarrow 352 = 2 \times \dfrac{{22}}{7} \times r$
On rearranging, we get-
$ \Rightarrow r = \dfrac{7}{{2 \times 22}} \times 352$
On solving, we get-
$ \Rightarrow r = 7 \times 8$
On multiplication, we get-
$ \Rightarrow r = 56$ m -- (ii)
Now we know that the circumference of the outer circle is=$2\pi R$ where R is the radius of outer circumference.
On putting the given values in the above formula we get-
$ \Rightarrow 396 = 2 \times \dfrac{{22}}{7} \times R$
On rearranging, we get-
$ \Rightarrow R = \dfrac{7}{{22 \times 2}} \times 396$
On solving, we get-
$ \Rightarrow R = 7 \times 9$
On multiplication, we get-
$ \Rightarrow R = 63$ m -- (iii)
On substituting values of eq. (ii) and eq. (iii) in eq. (i), we get-
$ \Rightarrow l = 63 - 56$
On subtraction, we get-
$ \Rightarrow l = 7$ m
The correct answer is option B.
Note: Here in this question it was also given to find the area of the racetrack then we would have found the area of the inner circumference and the outer circumference. Then subtract the area of inner circumference from outer circumference as the remaining area will be the area of the race track.