Question

A quadrilateral is a parallelogram if a pair of opposite sides are equal and parallel.

Answer 1

Hint: Here we are given a parallelogram where the opposite sides of it are equal and parallel. Our target is to prove that the other opposite is also equal. We use the conditions of congruence after drawing a diagonal and dividing the parallelogram into two triangles.

Complete step by step solution:

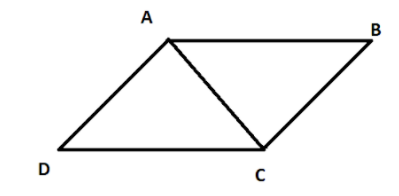
Given: ABCD is quadrilateral and.
To prove: ABCD is a parallelogram.

Proof:
As, AC is a transversal and also, therefore
\[\angle BAC = \angle DCA\] (As they are Alternate angles)
In \[\Delta ADC\] and ΔCBA, we have
\[AB = CD\] (Given)
\[\angle BAC = \angle DCA\] (Alternate angles)
\[AC = CA\] ( as, it is Common side)
Hence, by SAS rule, we get \[\Delta ADC \cong \Delta CBA\]
Hence, by corresponding parts of congruent triangles we get,\[DA = BC\]
Thus, Both the pair of opposite sides are equal in the quadrilateral ABCD, therefore ABCD is a parallelogram.
Hence we proved that a quadrilateral is a parallelogram if a pair of opposite sides are equal and parallel.

Note: There are six important properties of parallelograms to know:
1) Opposite sides are congruent (AB = DC).
2) Opposite angels are congruent (D = B).
3) Consecutive angles are supplementary \[\left( {A{\text{ }} + {\text{ }}D{\text{ }} = {\text{ }}180^\circ } \right).\]
4) If one angle is right, then all angles are right.
5) The diagonals of a parallelogram bisect each other.
6) Each diagonal of a parallelogram separates it into two congruent triangles.