Question

A quadrilateral ABCD is drawn to circumscribe a circle. Prove that \[AB+CD=AD+BC\].

Answer 1

Hint: We will suppose a circle with center as ‘O’ which is circumscribed by quadrilateral ABCD and the quadrilateral touches the circle at four points and then we will use the property of tangents of a circle that the lengths of tangents drawn from the external points are equal.

Complete step-by-step answer:
We have been given a quadrilateral ABCD circumscribing the circle then we have to prove that \[AB+CD=AD+BC\].
Let us suppose a circle with center ‘O’ which is circumscribed by the quadrilateral ABCD and touches the circle at point P, Q, R and S.

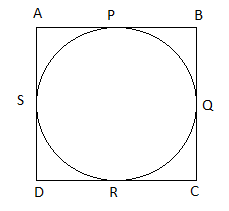
As we know that the length of tangents drawn from the external points are equal.
Therefore,
AP=AS…..(1)
BP=BQ…..(2)
DR=DS……(3)
CR=CQ…..(4)
Now adding equation (1), (2), (3) and (4) and we get as follows:
\[AP+BP+DR+CR=AS+BQ+DR+CQ\]
On rearranging the terms we get as follows:
\[\left( AP+BP \right)+\left( DR+CR \right)=\left( AS+DS \right)+\left( BQ+CQ \right)\]
Since we can see from the figure that,
AB=AP+BP
BC=BQ+CQ
CD=CR+DR
AD=AS+SD
Using these values, we get as follows:
AB+CD=AD+BC
Therefore, the required expression is proved.

Note: Remember the point that the length of a tangent from an external point to the circle is equal. In this question without a diagram we are unable to prove the given expression. So first of all draw the diagram according to the question.