Question

A pulley is attached to the ceiling of a lift moving upwards. Two particles are attached to the two ends of a massless string passing over the smooth pulley. The masses of the particles are in the ratio $2:1$. If the acceleration of the particles is $\dfrac{g}{2}$ w.r.t. lift, then the acceleration of the lift will be.
A. g
B. $\dfrac{g}{2}$
C. $\dfrac{g}{3}$
D. $\dfrac{g}{4}$

Answer 1

Hint: Concept of relative motion and the effect of acceleration of lift on the acceleration of the two masses is to be used. Then, it can be solved.

Complete step by step answer:
Let us consider that the acceleration of lift is as shown in figure.

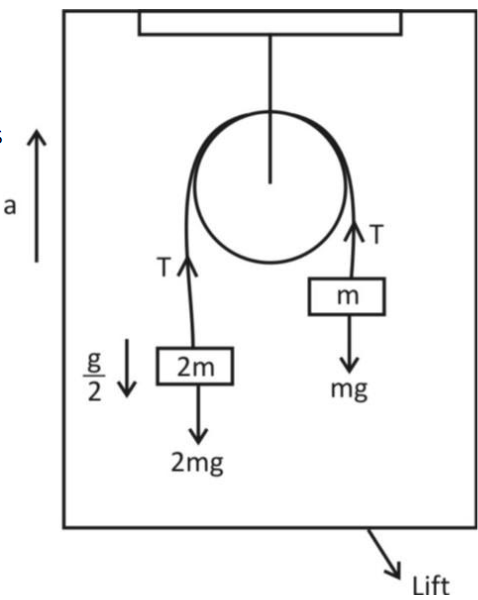
The mass $2$m being heavy, moves downward while mass m being small will move upward in an atwood machine.
Then, from figure we have acceleration of bigger mass (i.e. $2$m)$ = a - \dfrac{g}{2}$
Acceleration of smaller mass (i.e.m) $ = a + \dfrac{g}{2}$
There will develop a tension, T in the string as shown in figure. So, the equation form mass $2$m is,
$T - 2mg = 2m\left( {a - \dfrac{g}{2}} \right)$… (i)
And for mass, m is
$T - mg = m\left( {a + \dfrac{g}{2}} \right)$… (ii)
Subtracting equation (ii) from equation (i), we get
$T - 2mg - \left( {T - mg)} \right) = 2m\left( {a - \dfrac{g}{2}} \right) - m\left( {a + \dfrac{g}{2}} \right)$
$ \Rightarrow T - 2 mg - T + mg = 2ma - \dfrac{{2mg}}{2} - ma - \dfrac{{mg}}{2}$
$ \Rightarrow - mg = ma - \dfrac{{3mg}}{2}$
$ \Rightarrow ma = \dfrac{{3mg}}{2} - mg$
$ \Rightarrow ma = \dfrac{{3mg - 2mg}}{2} \Rightarrow ma = \dfrac{{mg}}{2}$
$ \Rightarrow a = \dfrac{g}{2}$
Hence, the acceleration of the lift will be $\dfrac{g}{2}$.

Note:
Here, as in the case of mass $2$m, both the acceleration a and $\dfrac{g}{2}$ are in the opposite direction.
So, net acceleration of $2m = a - \dfrac{g}{2}$
While in case of mass m, thay are in the same direction.
So, acceleration of small mass $ = a + \dfrac{g}{2}$.