Question

A proton in motion makes a head-on collision with an unknown particle at rest. If the collision is perfectly elastic and the proton rebounds back with $\dfrac{4}{9}$ of its initial kinetic energy after the collision, the mass of the unknown particle is
A. Equal to the mass of the proton
B. Twice the mass of the proton
C. 3 times the mass of the proton
D. 5 times the mass of the proton

Answer 1

Hint: In an elastic collision, when two bodies collide the total kinetic energy before collision will be equal to total kinetic energy after the collision. Since the second particle is at rest initially, the initial momentum of the proton will be equal to the final momentum of the two bodies.

Formula used: $K.E = \dfrac{1}{2} mu^2$
${m_1}{u_1}+{m_2}{u_2} = {m_1}{v_1}+{m_2}{v_2}$

Complete step-by-step solution:
The latest consider the proton to be a particle of mass m moving with initial velocity u.
The initial momentum of the system is just mu.
The initial kinetic energy of the system is
$\dfrac{1}{2} mu^2$

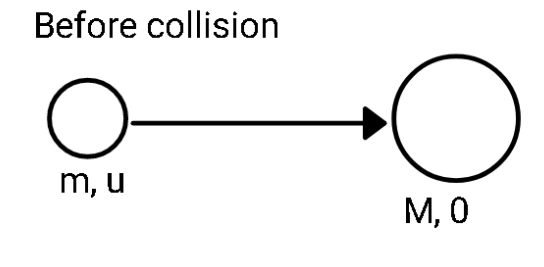
After the collision, the proton rebounds with the kinetic energy given as $\dfrac{4}{9}$ of initial kinetic energy. If the final velocity of the proton is v, then:
$\dfrac{1}{2}mv^2 = \dfrac{4}{9} \times \dfrac{1}{2} mu^2$
So we can write
$v = - \dfrac{2}{3}u$
Here negative sign is kept for the fact that the final velocity is in the opposite direction to the initial velocity.
By the use of conservation of momentum, we can write;
$mu = mv + MV$
Keeping the value of v here,
$mu = - \dfrac{2}{3}mu + MV$
$mu + \dfrac{2}{3}mu = MV$
$\dfrac{5}{3}mu = MV $
We can write this expression as:
$\dfrac{5m}{3M} = \dfrac{V}{u}$
Now, conservation of energy for the system gives:
$\dfrac{1}{2}mu^2 = \dfrac{1}{2} mv^2 + \dfrac{1}{2}MV^2$
Or as we previously obtained the value of final Kinetic energy of proton, we can write this as:
$\dfrac{1}{2}mu^2 \left( 1 - \dfrac{4}{9} \right) = \dfrac{1}{2}MV^2 $
$\dfrac{5}{9}mu^2 = MV^2 $
Making this in the ratio of velocities as we are about to substitute the previously obtained ratio.
$\dfrac{5m}{9M}= \dfrac{V^2}{u^2} $
Squaring the previous ratio of velocities and substituting, we get:
$\dfrac{5m}{9M}= \dfrac{25m^2}{9M^2} $
We get:
$1= \dfrac{5m}{M} $
$M = 5m$
Thus we get the mass of the heavier particles to be 5 times the mass of the proton.
Therefore the correct answer is an option (D).

Note: One might forget to account for the direction of velocity after collision. Therefore one can use vector notation or else one might obtain a wrong answer if anyway one does not include the negative of final velocity as compared to the initial velocity.