Question

A projectile is fixed at an angle $\theta $ with the horizontal, (as shown in the figure), condition under which it lands perpendicular on an inclined plane of inclination $\alpha $ is?

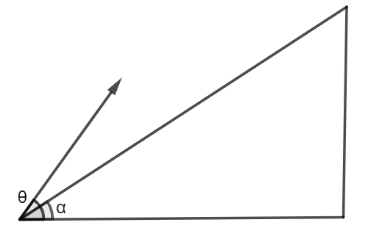
A. $\sin \,\alpha \, = \,\cos (\theta - \alpha )$
B. $\cos \,\alpha \, = \,\sin (\theta - \alpha )$
C. $2\tan \,\alpha \, = \,\cot (\theta - \alpha )$
D. $\cot (\theta - \alpha )\, = \,\sin \,\alpha $

Answer 1

Hint: Let us understand about the projectile motion. The motion experienced by a propelled target is known as projectile motion. Ballistics is a branch of dynamics that studies the movement, actions, and effects of projectiles, such as bullets, unguided explosives, rockets, and the like; it is also the science or art of designing and accelerating projectiles to achieve a desired result.

Complete step by step answer:

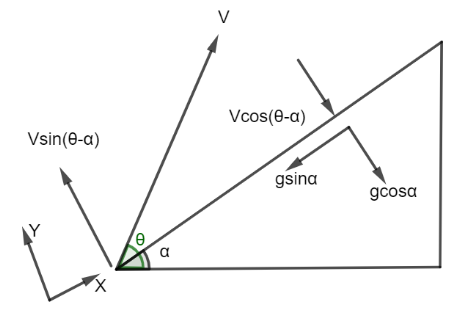
The time of flight (T) is calculated by looking at motion in the y-axis (which is no more vertical as in the normal case). The y-direction displacement after the projectile has returned to the incline, on the other hand, is zero, as it is in the usual case.For $y = 0$, use the equation of motion perpendicular to the incline.
$y = {v_y} \times T + \dfrac{1}{2} \times {a_y}{T^2} = 0$
$ \Rightarrow \,v\sin (\theta - \alpha )T + \dfrac{1}{2}( - g\cos \alpha ){T^2} = 0$
$ \Rightarrow T\left\{ {\,v\sin (\theta - \alpha ) + \dfrac{1}{2}( - g\cos \alpha )T} \right\} = 0$
Either,$T = 0,$
$ \Rightarrow T = \dfrac{{2v\sin (\theta - \alpha )}}{{g\cos \alpha }}$
Time is given as,
$v = u + at$
$\Rightarrow 0 = v\,\cos (\theta - \alpha ) - (g\,\sin \alpha )t$
$\Rightarrow t = \dfrac{{v\cos (\theta - \alpha )}}{{g\cos \alpha }}$
As we know that the both times are equal so, it can be written as,
$\dfrac{{v\cos (\theta - \alpha )}}{{g\cos \alpha }} = \dfrac{{2v\sin (\theta - \alpha )}}{{g\cos \alpha }}$
$\therefore \cot (\theta - \alpha ) = 2\tan \alpha $

Hence, option C is correct.

Note: Let us know about a special case of trajectory. A lofted trajectory, or one with an apogee greater than the minimum-energy trajectory to the same height, is a special case of a ballistic trajectory for a rocket. To put it another way, the rocket flies higher and hence expends more energy to reach the same landing spot. This can be achieved for a variety of purposes, including raising the distance to the horizon to increase viewing/communication range or adjusting the angle at which a missile can land. In both missile rocketry and spaceflight, lofted trajectories are occasionally used.