Question

A powder tin has a square base with side $12cm$and height $17.5cm$. Another is cylindrical with diameter of its base $12cm$and height $17.5cm$.Which has more capacity and how much?

Answer 1

Hint:
capacity indicates the volume capacity of cuboid and cylinder, find the volume of cuboid$(Volum{e_{cuboid}} = l \times b \times h)$and find the volume of the cylinder$\left( {Volum{e_{cylinder}} = \pi {r^2}h} \right)$.Find which of them has more capacity and find the difference between them.

Complete step by step solution:

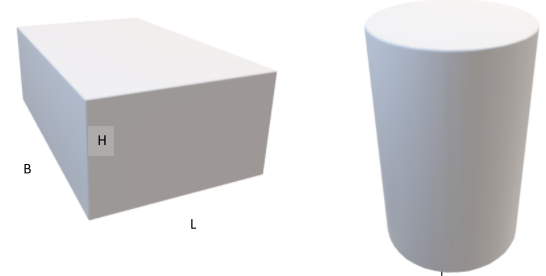
Now, let’s find the volume of the cuboid,
Given that base is square of side $12cm$and height$17.5cm$, then $Volum{e_{cuboid}} = l \times b \times h$
Where,$l$ =length
             $b$=breadth
             $h$ =height
$
   \Rightarrow Volum{e_{cuboid}} = l \times b \times h \\
  \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 12 \times 12 \times 17.5 \\
  \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2520c{m^3}...........\left( 1 \right) \\
 $
Now, let’s find the volume of the cylinder,
Given that the diameter of the base is $12cm$and height is $17.5cm$, then the $\left( {Volum{e_{cylinder}} = \pi {r^2}h} \right)$
Where,$r$=Radius
              $h$=height
And, $r = \dfrac{d}{2} = \dfrac{{12}}{2} = 6cm$
\[
 \Rightarrow Volum{e_{cylinder}} = \pi {r^2}h \\
= \dfrac{{22}}{7} \times {6^2} \times 17.5 \\
 = 1980c{m^3}.........\left( 2 \right) \\
 \]
So, from (1) and (2) Cuboid has more capacity than cylinder
And the difference between their capacity is=$2520 - 1980 = 540c{m^3}$

So, cuboid has more capacity than cylinder by $540c{m^3}$.

Note:
Analyze which 3D shape will form from the given description and check the requirements during applying the formula, especially during diameter and radius.