Question

A portion of a \[60\]m long tree is broken by a tornado and the top struck up the ground making an angle of ${30^ \circ }$ with the ground level. Find the height of the point where the tree is broken.

Answer 1

Hint:
Assume the height of the point where the tree is broken to be x m. Then use the formula of $\sin \theta = \dfrac{{{\text{Height of tree}}}}{{{\text{Hypotenuse}}}}$ where height of the tree is perpendicular here. Then use the value of trigonometric ratio$\sin {30^ \circ } = \dfrac{1}{2}$. Put all the values in the formula and solve for x.

Complete step by step solution:
 Given, the total height of tree (AB) =\[60\]m
This tree is broken by the tornado at point C and the top A stuck up the ground making an angle of ${30^ \circ }$ with ground level.
We have to find the height of the point where the tree is broken. Let this height be x m.
Then we can write,
AB=AC+CB
On putting values we get,
$ \Rightarrow 60 = CA + x$
Then we get,
$ \Rightarrow $ CA=$60 - x$

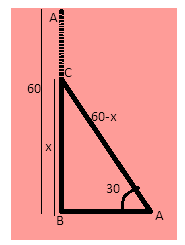
Now in \[\Delta CBA\],
CB=x m, CA=$\left( {60 - x} \right)$ and $\angle CAB = {30^ \circ }$
Then on using formula-
$\sin \theta = \dfrac{{{\text{Height of tree}}}}{{{\text{Hypotenuse}}}}$
Because the height CB is the perpendicular in the triangle.
On putting the values we get,
$ \Rightarrow \sin {30^ \circ } = \dfrac{{CA}}{{CB}}$ ---- (i)
We know that$\sin {30^ \circ } = \dfrac{1}{2}$and CA=x m and CB=$60 - x$ m
On putting these values in the eq. (i) we get,
$ \Rightarrow \dfrac{1}{2} = \dfrac{x}{{60 - x}}$
On cross multiplication we have,
$ \Rightarrow 60 - x = 2x$
On solving we get,
$ \Rightarrow 60 = 2x + x$
On addition we get,
$ \Rightarrow 60 = 3x$
$ \Rightarrow x = \dfrac{{60}}{3} = 20$

Hence, the length of the point at which the tree is broken is $20$ m.

Note:
Here we have used the formula of sin ratio instead of cosine ratio because in sine ratio we know all the values involved. But if we use cosine ratio then the formula becomes-
$ \Rightarrow \cos \theta = \dfrac{{BA}}{{CA}}$
Here we don’t know the value of AB so we cannot solve the equation. Hence we use the formula of sine ratio.