Question

A pole is standing erect on the ground which is horizontal. The tip of the pole is tied right with a rope of $\sqrt {12} m$ to a point on the ground. if the rope is making 30° angle with the horizontal, then the height of the pole is
A. 2$\sqrt 3 $m
B. 3$\sqrt 2 $ m
C. 3m
D. $\sqrt 3 $m

Answer 1

Hint: In this question first of all make a diagram to get a visual picture of the problem, then assume the height to be H. Now use properties of the trigonometric ratios i.e. in this case Sin$\theta $=$\dfrac{{Perpendicular}}{{{\text{Hypotenuse}}}}$. This will help you to find the height (perpendicular).

Complete step-by-step answer:
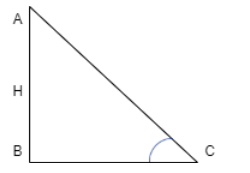
Let the height of the pole be H metres
According to the question AC=$\sqrt {12} m$
We know by basic properties of trigonometric ratios that Sin$\theta $=$\dfrac{{Perpendicular}}{{{\text{Hypotenuse}}}}$
In triangle ABC,
Sin 30\[^0\]=$\dfrac{H}{{AC}}$
Sin 30\[^0\] = $\dfrac{H}{{\sqrt {12} }}$
We know that Sin 30\[^0\] = $\dfrac{1}{2}$
$\dfrac{1}{2}$=$\dfrac{H}{{\sqrt {12} }}$
H= $\dfrac{{\sqrt {12} }}{2}$
H=$\dfrac{{\sqrt {4 \times 3} }}{2}$
H=$\dfrac{{2\sqrt 3 }}{2}$
H=$\sqrt 3 $
So, the height of the triangle is $\sqrt 3 $m.

Note: The ratios of the sides of a right triangle are called trigonometric ratios. There are six trigonometric ratios, sine, cosine, tangent, cosecant, secant and cotangent. These six trigonometric ratios are abbreviated as sin, cos, tan, csc, sec, cot.