
A point
a)
b)
c)
d) 2
Answer
511.2k+ views
Hint: We have the following expression:
As we know that, the greatest integer function returns the nearest integer value. So, [1] = 1. Therefore, the expression can be written as:
If a function lies in the interval
Complete step-by-step solution:
We are having a greatest integer function as:
Since, we know that [1] = 1, we can write equation (1) as:
As we know that,
Now, using the above result, we can find the value of
Case-I: When
So, we can write:
Therefore,
As we have,
So, we can say that:
Case-I: When
So, we can write:
Therefore,
As we have,
So, we can say that:
So, from equation (3) and (4), we can plot a graph using the interval
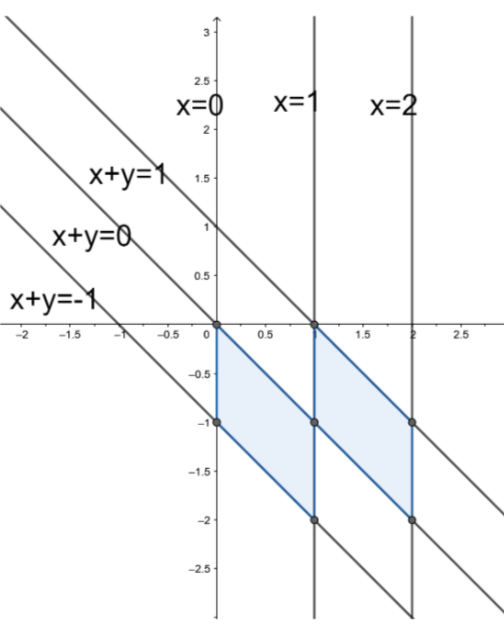
Hence, we need to find the area of the shaded region in the above graph. This region has four triangles of the same base and the same height.
So, the area of shaded region = 4
Hence, option (d) is the correct answer.
Note: The Greatest Integer function is given as:
For example:
As we know that, the greatest integer function returns the nearest integer value. So, [1] = 1. Therefore, the expression can be written as:
If a function lies in the interval
Complete step-by-step solution:
We are having a greatest integer function as:
Since, we know that [1] = 1, we can write equation (1) as:
As we know that,
Now, using the above result, we can find the value of
Case-I: When
So, we can write:
Therefore,
As we have,
So, we can say that:
Case-I: When
So, we can write:
Therefore,
As we have,
So, we can say that:
So, from equation (3) and (4), we can plot a graph using the interval

Hence, we need to find the area of the shaded region in the above graph. This region has four triangles of the same base and the same height.
So, the area of shaded region = 4
Hence, option (d) is the correct answer.
Note: The Greatest Integer function is given as:
For example:
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Which one is a true fish A Jellyfish B Starfish C Dogfish class 11 biology CBSE

The flightless birds Rhea Kiwi and Emu respectively class 11 biology CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




