Question

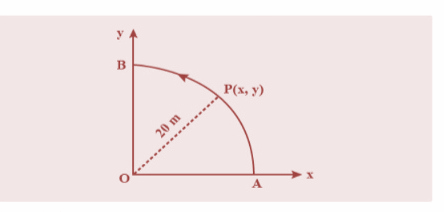
A point P moves in counter-clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out a length $ = {t^3} + 5$ , where s is in metres and t is in seconds. The radius of the path is 20m. The acceleration of P when t=2s is nearly :

A. $13m/{s^2}$
B. $12m/{s^2}$
C. $7.2m/{s^2}$
D. $14m/{s^2}$

Answer 1

Hint: The capacity of the vehicle to increase or gain the speed is known as acceleration. Velocity is the prime indicator of the direction. By applying the velocity and acceleration formula we can solve the above problem.

Formula used:
Velocity, ${\text{v = }}\dfrac{{{\text{ds}}}}{{{\text{dt}}}}$
Acceleration, ${{\text{a}}_t}{\text{ = }}\dfrac{{{\text{dv}}}}{{{\text{dt}}}}$
Centripetal acceleration, ${{\text{a}}_{\text{c}}}{\text{ = }}\dfrac{{{{\text{v}}^{\text{2}}}}}{{\text{R}}}$
Net acceleration, $a = \sqrt {\left( {{a^2}_t + {a^2}_c} \right)} $
Where, s is the displacement, t is the time taken, R is the radius, ${a_t}$is tangential acceleration.
Given, A point P moves in counter-clockwise direction on a circular path of radius r=20m. and displacement $s = {t^3} + 5$.

Complete step-by-step answer:
We need to calculate acceleration of P at time t=2s.
Let us consider a given equation,
$s = {t^3} + 5$
Velocity ${\text{v = }}\dfrac{{{\text{ds}}}}{{{\text{dt}}}}$
$v = \dfrac{{d\left( {{t^3} + 5} \right)}}{{dt}} = 3{t^2}$
And let us consider rate of change of velocity, acceleration ${\text{a = }}\dfrac{{{\text{dv}}}}{{{\text{dt}}}}$
We can substitute the value of v in the above equation, we get,
${\text{a = }}\dfrac{{{\text{d}}\left( {{\text{3}}{{\text{t}}^{\text{2}}}} \right)}}{{{\text{dt}}}}{\text{ = 6t}}$
Therefore tangential acceleration at t=2 second
Then, ${a_t} = 6 \times 2 = 12m{s^{ - 2}}$
${v^2} = 3{t^2} = 3 \times 4 = 12m{s^{ - 1}}$
Now centripetal acceleration, ${{\text{a}}_{\text{c}}}{\text{ = }}\dfrac{{{{\text{v}}^{\text{2}}}}}{{\text{R}}}$
${{\text{a}}_{\text{c}}}{\text{ = }}\dfrac{{{{12}^2}}}{{20}} = \dfrac{{144}}{{20}} = 7.2{\text{m}}{{\text{s}}^{{\text{ - 2}}}}$
Therefore, net acceleration $a = \sqrt {\left( {{a^2}_t + {a^2}_c} \right)} $
$a = \sqrt {\left( {{{12}^2} + {{7.2}^2}} \right)} = 14{\text{m}}{{\text{s}}^{{\text{ - 2}}}}$
Thus, acceleration of point P when t=2 s is nearly $14{\text{m}}{{\text{s}}^{{\text{ - 2}}}}$.
Therefore, correct option is (D).
Additional information:
When a particle moves along a circular path, the line joining the particle to the axis of rotation is called radius vector. The angle described by the radius vector in a given time is called the angular displacement. It is measured in radians. The rate of angular displacement is called angular velocity.
The motion of a particle along the circumference of a circle with uniform angular velocity is called uniform circular motion.
During uniform circular motion the radius vector describes equal angular displacement in equal intervals of time. Hence, the particle moves along the circular path with constant speed. But there is a continuous change in direction. The velocity of the particle at any point on the circular path is along the tangent to the circular path at that point.
When a particle is having uniform circular motion there is a continuous change in direction, even though the distance travelled per unit time (speed) remains constant. Hence, the particle has a variable velocity which gives rise to an acceleration. This acceleration must be perpendicular to the path because the speed of the particle is constant. For uniform circular motion, the acceleration is directed towards the centre at every instant
When a particle is having uniform circular motion, the acceleration of the particle which is acting along the radius towards the centre of the circular path is called centripetal acceleration. Centripetal acceleration, ${{\text{a}}_{\text{c}}}{\text{ = }}\dfrac{{{{\text{v}}^{\text{2}}}}}{{\text{R}}}$
If a body moves in a circular path with changing speed it possesses (i) tangential acceleration (ii) radial acceleration and(iii) angular acceleration.
Note:In the acceleration motion, the circular motion constantly changes its speed. To maintain the spin, motion the centripetal force is required.