Question

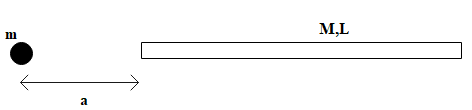
A point mass $m$ and a uniform thin rod (mass $M$ and length $L$) are shown in figure. Find the gravitational force of attraction between them.
A.$\dfrac{GMm}{{{a}^{2}}}$
B.$\dfrac{GMm}{a\left( a+L \right)}$
C.$\dfrac{GMm}{{{\left( a+L \right)}^{2}}}$
D.$\dfrac{4GMm}{{{\left( 2a+L \right)}^{2}}}$

Answer 1

Hint: Each element of the given rod is not at the same distance from the given point mass. Therefore, the force of gravitation exerted by the rod will not be constant throughout the rod. In such a case, we shall take an infinitesimally small element of the rod and find the force it applies on the point mass. Further, this infinitesimally small force is integrated throughout the length of road to find total force on the point mass.

Complete answer:
Gravitational force on a point mass is given as:
$F=\dfrac{G{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}$
Where,
$G=6.67\times {{10}^{-11}}N{{m}^{2}}k{{g}^{-2}}$ = universal gravitational constant
${{m}_{1}}=$ mass of one body
${{m}_{2}}=$ mass of second body
$r=$ distance between their respective centre of masses
We are given a thin uniform rod of mass $M$ and length $L$. Let us take an element $dx$ at a distance $x$ from the point mass.

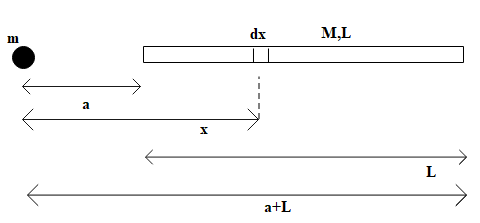
The mass $dm$ of this element is given as:
$dm=\lambda .dx$
Where, $\lambda =$ linear mass density of rod.
$\therefore \lambda =\dfrac{M}{L}$
$\Rightarrow dm=\dfrac{M}{L}.dx$
Therefore, the force on the point by this small element is given as:
$dF=\dfrac{Gm.dm}{{{x}^{2}}}$
We shall now integrate this infinitesimally small force to find the total force on the point mass due to the rod. Since the distance of interaction of rod varies from distance $a$ to $\left( a+L \right)$,
  \[\begin{align}
  & \Rightarrow \int{dF}=\int\limits_{a}^{a+L}{\dfrac{Gm.dm}{{{x}^{2}}}} \\
 & \Rightarrow \int{dF}=\int\limits_{a}^{a+L}{\dfrac{Gm}{{{x}^{2}}}\left( \dfrac{M}{L}dx \right)} \\
 & \Rightarrow \int{dF}=\int\limits_{a}^{a+L}{\dfrac{GMm}{L{{x}^{2}}}.dx} \\
\end{align}\]
\[\Rightarrow \int{dF}=\dfrac{GMm}{L}\int\limits_{a}^{a+L}{\dfrac{dx}{{{x}^{2}}}}\]
\[\begin{align}
  & \Rightarrow F=\dfrac{GMm}{L}\left( \dfrac{-1}{x} \right)_{a}^{a+L} \\
 & \Rightarrow F=\dfrac{-GMm}{L}\left( \dfrac{1}{a+L}+\dfrac{1}{a} \right) \\
\end{align}\]
\[\begin{align}
  & \Rightarrow F=\dfrac{-GMm}{L}\left( \dfrac{a-\left( a+L \right)}{a\left( a+L \right)} \right) \\
 & \Rightarrow F=\dfrac{-GMm}{L}\left( \dfrac{-L}{a\left( a+L \right)} \right) \\
 & \Rightarrow F=\dfrac{GMm}{a\left( a+L \right)} \\
\end{align}\]

Therefore, the correct option is (B)\[\dfrac{GMm}{a\left( a+L \right)}\].

Note:
Force of gravitation acting between two bodies is usually an attractive force which pulls the bodies mutually towards each other. This is the force which binds us to the Earth and does not let us float in the air. We apply the same amount of attractive force on the earth as the Earth applies on us. However, this is ignored because of the massive size of the Earth that force applied on it does not have any affect on it.