Question

A planet is moving around the Sun in a circular orbit of circumference $C$. The work done on the planet by the gravitational force $F$ of the Sun is $kFC$, then what is the value of $k$?

Answer 1

Hint: The gravitational force of the sun pulls the planet inward along the line joining between the centers of the planet and the sun. Hence the motion of the planet is circular; you can say that this distance is actually the radius of the orbit of the planet around the sun. Similarly moving around a fixed orbit in a circular path, shows that the motion is uniform circular motion. Here the only force that comes into play is the gravitational force of the sun on the planet, which keeps the planet constantly rotating along a fixed orbit around the sun.

Formula used:
The work done $W$ by a force $\overrightarrow F $ that causes a displacement $\overrightarrow S $is
\[W = \overrightarrow F \cdot \overrightarrow S = FS\cos \theta \] (1)
where $\theta $ is the angle between the direction vectors of the force and the displacement of the planet.

Complete step by step answer:
Given:
The gravitational force on the planet due to the sun is $F$.
The circumference of the circular orbit in which the planet rotates around the sun is $C$.
The work done on the planet by the gravitational force $F$ of the sun is $kFC$.

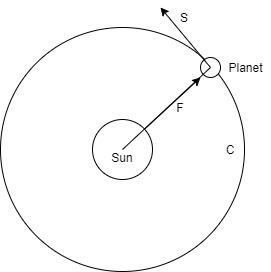
To get: The value of $k$.
Step 1:
You can see that the gravitational force $F$ is acting on the sun along the radius of the orbit with the circumference $C$.
But, the displacement of the planet at each instance of the time is along the tangential direction to the circular orbit, as the planet is in a uniform circular motion.
Hence, you can get that the direction along the displacement of the planet is perpendicular to the direction along which the gravitational force of the sun on the planet, $F$acts.
So, you get the value of the angle $\theta $ as ${90^ \circ }$.

Step 2:
Now putting the angle $\theta $in eq (1), you can see that the work done by the gravitational force $F$of the sun on the planet becomes
$ W = FS\cos \theta $
$ = FS\cos {90^ \circ } $
$ = FS \times 0 $
$ = 0 $

Step 3:
You are given the work done to be $W = kFC$ as well.
Now compare the two values of the work done $W$.
$kFC = 0$
Now, $F$ and $C$ possess non-zero values. So, the only term left is $k$.
$\therefore k = 0$

If a planet is moving around the Sun in a circular orbit of circumference $C$ and the work done on the planet by the gravitational force $F$ of the Sun is $kFC$, then the value of $k$ should be $0$.

Note:
While calculating the work done by any force, remember the work done is a dot product of the force vector $\overrightarrow F $ and the displacement vector $\overrightarrow S$. Hence, for such questions where only magnitudes are given, you have to identify the direction along which the force is acted upon and the direction along which the body displaces, otherwise, there shall be a mistake.
Again, without calculating you can also predict the work done $W$ to be $0$ here. You know that centripetal force does not work on the body under the uniform circular motion for the same logic that you saw above. Here, the gravitational force $F$ by the sun on the planet acts as the centripetal force to keep the planet rotating along the circular orbit. So, you can safely predict the work done $W$ by the gravitational force $F$, which is the centripetal force here, is nothing but $0$.
So, trivially the value of $k$ should be $0$.