Question

A piezoelectric quartz crystal of thickness $0.005m$ is vibrating in resonance conditions. Calculate the fundamental frequency ${f_0}$ for quartz ($Y = 8 \times {10^{10}}N{m^{ - 2}}$ and $\rho = 2.56 \times {10^3}$ )
A) $5.5MHz$
B) $55MHz$
C) $0.55MHz$
D) $5.5kHz$

Answer 1

Hint:First we have to find the speed of sound waves in quartz crystals by using the relation between frequency and velocity of waves. We know that the fundamental frequency length or thickness of the medium must be half of the wavelength of the wave.

Step by step solution:
Step 1
Velocity of wave in quartz crystal $v = \sqrt {\dfrac{Y}{\rho }} $
Where $Y \Rightarrow $ young modulus for medium
$\rho \Rightarrow $ Density of medium
$ \Rightarrow v = \sqrt {\dfrac{{8 \times {{10}^{10}}}}{{2.65 \times {{10}^3}}}} $
Solving this
$ \Rightarrow v = \sqrt {3.01 \times {{10}^7}} $ M/sec
Step 2
We know the relation between velocity of wave, frequency and wavelength is given as
$v = f\lambda $ .................. (1)
Where $f \Rightarrow $ frequency of wave
$\lambda \Rightarrow $ Wavelength of wave
For fundamental frequency the length or thickness must be equal to half of wavelength
\[ \Rightarrow L = \dfrac{\lambda }{2}\]
$ \Rightarrow \lambda = 2L$
Where $L \Rightarrow $ thickness of quartz crystal
From equation (1)
$ \Rightarrow {f_0} = \dfrac{v}{\lambda }$
$ \Rightarrow {f_0} = \dfrac{v}{{2L}}$
Put the value of velocity and thickness $L = 0.005m$
$ \Rightarrow {f_0} = \dfrac{1}{{2 \times 0.005}}\sqrt {3.01 \times {{10}^7}} $
$ \Rightarrow {f_0} = \dfrac{{5.4 \times {{10}^3}}}{{10 \times {{10}^{ - 3}}}}$
Further solving
$ \Rightarrow {f_0} = 0.54 \times {10^6}$
Hence
$\therefore {f_0} = 0.55MHz$

Hence option C is correct.

Note:By this simple method we can calculate the fundamental frequency .We use here for fundamental frequency the wavelength must be double of length of medium as shown in figure

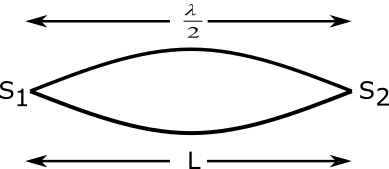
For fundamental vibration $L = \dfrac{\lambda }{2}$ it is clear from the above diagram.