Question

What is a piecewise continuous function?

Answer 1

Hint: For solving this type of question you should know about the piecewise continuous function and its properties. The piecewise continuous function is generally defined as a function that has a finite number of breaks in the function and doesn’t blow up to the infinity anywhere. It means this is a piecewise function but it does not go to the infinity.

Complete step by step answer:
The piecewise continuous function is a function which is called piecewise continuous on a given interval and if the interval can be broken into a finite number of subintervals on which the function is continuous on each open subinterval and it has a finite limit at the endpoints of each subinterval. The piecewise continuous function is shown in the figure below:

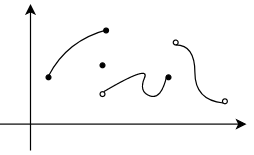
We can say that the piecewise continuous function has a finite number of breaks and it doesn’t go to infinity. For example, if we consider a function,
$s\left( x \right)=\left\{ \begin{align}
  & -\text{1if }x<0 \\
 & \text{0 if }x=0 \\
 & \text{1 if }x>0 \\
\end{align} \right.$
The function is continuous for all $x\in R$ except $x=0$.
The function is discontinuous at $x=0$ and we cannot remove it. We cannot redefine $s\left( x \right)$ at that point and get a continuous function. So,
$\begin{align}
  & \displaystyle \lim_{s \to {{0}^{+}}}s\left( x \right)=1 \\
 & \displaystyle \lim_{s \to {{0}^{-}}}s\left( x \right)=-1 \\
\end{align}$
At $x=0$, the graph of the function jumps. So, the left and right limits disagree with one another and with the value of the function at $x=0$in our example, the definition of $s\left( x \right)$ as a function from $\left( -\infty ,0 \right)\cup \left( 0,\infty \right)\to R$ is continuous. If the graph $s\left( x \right)$ is restricted to this domain, it still looks like it is discontinuous at 0, but 0 is not a part of the domain, so the function is continuous.

Note: For solving these questions the intervals in which the function is defined are very much important because defining any function in any interval shows that the function is continuous at that value or not and is the function going to infinity or not which decides the continuity of a function.