Question

A piece of wire in the form of the rectangle of the length $7cm$ and breadth $4cm$ is refolded in the form of the circle. Find the radius of the circle.

Answer 1

Hint:
When we change the shape of the wire from rectangle to the circle then the total length of both the parts do not change which means that the circumference of both the shapes are equal and we know that the perimeter of the rectangle is $2(l + b)$ and the circumference of circle is $2\pi R$

Complete step by step solution:
Here we are given that piece of wire in the form of the rectangle of the length $7cm$ and breadth $4cm$ is refolded in the form of the circle so now we can say that the both will have the same length of the total boundary as the wire is same which is refolded into the different shapes.
Let the radius of the wire be $R$ and the total length of the wire be $L$ and we are converting the same wire from rectangle to the circle that is

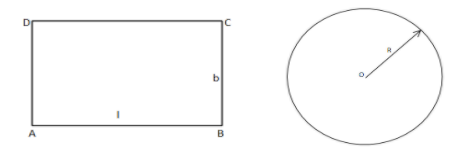
Here $ABCD$ is the rectangle formed by the piece of the wire that is converted to the circle with the centre O and radius $R$ and as now we have assumed that the total length of the wire is $L$ and the total length would be equal to the perimeter of the rectangle.
So ${\text{total length of the wire}} = {\text{perimeter of the rectangle ABCD}}$
And we know that the perimeter of the rectangle is given by $2(l + b)$ and in this question $l = 7cm,b = 4cm$
So total length of piece of wire$L = 2(l + b)$
$
   = 2(7 + 4)cm \\
   = 2(11) \\
   = 22cm \\
 $
When we change the shape, then the total length of wire will remain the same and will become equal to the circumference of the circle which is given by $2\pi R$
So we can say that
$
  2\pi R = L \\
  2\pi R = 22 \\
  2\left( {\dfrac{{22}}{7}} \right)R = 22 \\
  R = \dfrac{7}{2} = 3.5cm \\
 $

So we get the radius of the circle as $3.5cm$.

Note:
If a bowl of the certain shape contains water and now if we pour that water into the different shape then the volume occupied by the water in both the shapes will be equal and we know that the volume of the cuboid$ = lbh$ and volume of the cylinder$ = \pi {R^2}h$