Question

A picture is painted on cardboard $8cm$ long and $5cm$ wide such that there is a margin of $1.5cm$ along each of its sides. Find the total area of the margin.

Answer 1

Hint: We will draw a pictorial representation of the given condition and from the figure, we can say that the area of the margin will be equal to the difference between the total area of the cardboard and the area excluding the marginal length. The area of the cardboard will be equal to the area of a rectangle given by the formula: Area of the rectangle = $l \times b$, where l is the length and b is the breadth of the cardboard.

Complete step-by-step answer:
 We are given a picture painted on a cardboard whose length is $8cm$ and breadth is $5cm$. There is a margin of $1.5cm$ along each side of the cardboard.
We are required to calculate the total area of the margin.
The figure of this situation will be:

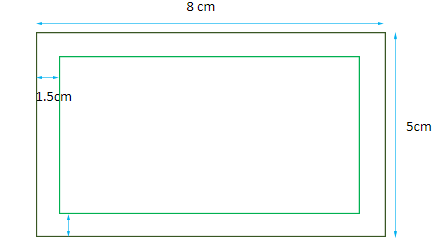
From the figure, we can see that the area of the margin can be calculated by subtracting the area of the inner rectangle from the cardboard (or outer rectangle).
The dimensions of the inner rectangle will be:
Length of the inner rectangle = $8 - \left( {1.5 + 1.5} \right) = 8 - 3 = 5cm$
Breadth of the inner rectangle = $5 - \left( {1.5 + 1.5} \right) = 5 - 3 = 2cm$
Therefore, the inner rectangle is $5cm$ long and $2cm$ wide.
So, the area of the margin = area of the outer rectangle – area of the inner rectangle.
The area of the rectangle is given by the formula: $l \times b$, where l is the length and b is the breadth of the cardboard.
Therefore, the area of the margin = $\left( {8 \times 5} \right) - \left( {5 \times 2} \right)$
$ \Rightarrow $ The area of the margin = $40 - 10 = 30c{m^2}$
Hence, the total area of the margin of the painting on the cardboard is found to be $30c{m^2}$.


Note: In this question, you may get confused in the step where we have deduced from the figure that the area of the margin is the difference between the areas of the original cardboard and the remaining portion after excluding the marginal part. Also, for the dimensions of the inner rectangle (or the portion after excluding the margins) are taken in such a way because the margins are along every side and hence, we have to exclude them from the top – bottom and from left – right sides and that’s why we have subtracted them twice from the original dimensions of the cardboard.