Question

A pendulum bob has a speed of $3\,m/s$ while passing through its lowest position, length of the pendulum is $0.5\,m$ then its speed when it makes an angle of 60\[^ \circ \] with vertical is:
A. 2 m/s
B. 1 m/s
C. 4 m/s
D. 3 m/s

Answer 1

Hint: To solve this question we need a basic understanding about LAW OF CONSERVATION OF ENERGY. But as an angle of \[{60^ \circ }\] is made with the vertical before applying the law of conservation of energy we need to resolve it into its respective components and then solve it.

Formula used:
\[K{E_i} + P{E_i} = K{E_f} + P{E_f} - - - - - - (1)\]
Where, \[K{E_i} = \]initial kinetic energy, \[P{E_i} = \]initial potential energy, \[P{E_f} = \]final potential energy and \[K{E_f} = \]final kinetic energy.

Complete step by step answer:
At the highest point at a pendulum the pendulum is momentarily stationary. Hence it has only potential energy at that point. Whereas at the lowest point it has very high speed that it has maximum kinetic energy. Hence this way we see that the pendulum's total mechanical energy is based on a combination of both KE and PE.Generally potential energy is given by:
\[PE = mgh\]

But in this question it has been given that it is making an angle \[{60^ \circ }\] vertically.Hence we express height in terms of length(L) and angle \[\theta \]. To get a better idea look at the following image:

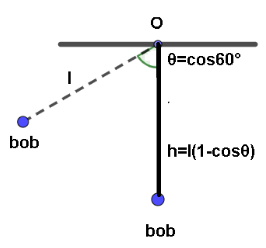
Hence we get;
\[h = L\left( {1 - \cos \theta } \right) - - - - - - (2)\].
Also the speed of the pendulum (v) , its length(L) and angle \[\theta \] have been given.
Hence the kinetic energy at the lowest position is given by:
\[KE = \dfrac{1}{2}m{v^2}\]
\[ \Rightarrow KE = \dfrac{9}{2}m\]
\[ \Rightarrow KE = \dfrac{1}{2}m{\left( 3 \right)^2}\]
When the pendulum makes an angle \[{60^ \circ }\] the pendulum has both KE and PE. Thus we have to find h using equation2,
Therefore: \[h = l\left( {1 - \cos \theta } \right)\]
\[ \Rightarrow h = 0.5\left( {1 - \cos {{60}^ \circ }} \right)\]
\[ \Rightarrow h = 0.5\left( {1 - \dfrac{1}{2}} \right)\]
\[ \Rightarrow h = \dfrac{1}{4}\].

Then the total energy of the bob is :
\[E = \dfrac{1}{2}m{v^2} + mgh\]
Substitute the values:
\[E = \dfrac{1}{2}m{v^2} + mgh\]
\[ \Rightarrow E = \dfrac{1}{2}m{v^2} + m \times 10 \times \dfrac{1}{4}\]
\[ \Rightarrow E = \dfrac{1}{2}m{v^2} + m \times \dfrac{5}{2}\]
Therefore by the use of law of conservation of energy
\[\dfrac{9}{2}m = \dfrac{1}{2}m{v^2} + m\dfrac{5}{2}\]
\[ \Rightarrow \dfrac{{9m}}{2} - \dfrac{{5m}}{2} = \dfrac{1}{2}m{v^2}\]
\[ \Rightarrow \dfrac{4}{2} = \dfrac{1}{2}{v^2}\]
\[ \Rightarrow 4 = {v^2}\]
\[ \therefore v = 2\,m/s\].

Hence the correct answer is option A.

Note: The pendulum mentioned here is a simple pendulum which also has a bob attached to a light inextensible string revolving in a horizontal circular motion. It revolves around a vertical axis. A pendulum is suspended from a pivot point.