Question

A particle starting from the origin $(0,0)$ moves in a straight line in the x-y plane.Its coordinates at a later time are \[(\sqrt 3 ,3)\]. The path of particle makes with x axis at an angle of
A. $30^\circ $
B. $60^\circ $
C. $45^\circ $
D. $0^\circ $

Answer 1

Hint: In order to solve this question we need to understand the straight line definition which states that a straight line is a path traced by particles in moving from one point to another such that direction of motion is constant. We can derive a straight line equation of the body by finding slope or the angle from the x axis which is made while moving.

Complete step by step answer:
According to the given problem, let the origin be denoted by point $O$ and at a later time its position denoted by point $A$. So connecting these two points we get a straight line making an angle $\theta $ with an $x$ axis.

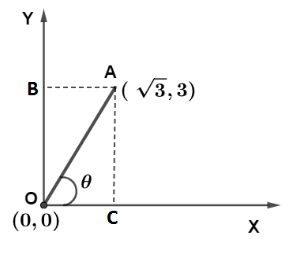
Since the coordinate of point A is $(\sqrt 3 ,3)$
Hence OC is $\sqrt 3 $ and OB is $3$
Now since the vector can be linearly translated so $OB = AC$
Now in triangle $\Delta OAC$ from trigonometry we have $\tan \theta = \dfrac{{AC}}{{OC}}$
$\tan \theta = \dfrac{3}{{\sqrt 3 }} = \sqrt 3 $
So inverting it we get $\theta = {\tan ^{ - 1}}(\sqrt 3 ) = 60^\circ $

So the correct option is B.

Note: It should be remembered that this problem could also be solved using a straight line equation that is $y = mx$ where “m” is slope of line or tangent of angle which it makes with x axis. Also slope is defined as derivative of equation $y = mx$ which can simply written as $m = \dfrac{{dy}}{{dx}}$ where $dy$ is the change in magnitude of parameter on y axis while between two points and similarly $dx$ is the change in magnitude of parameter on x axis between two points.