Question

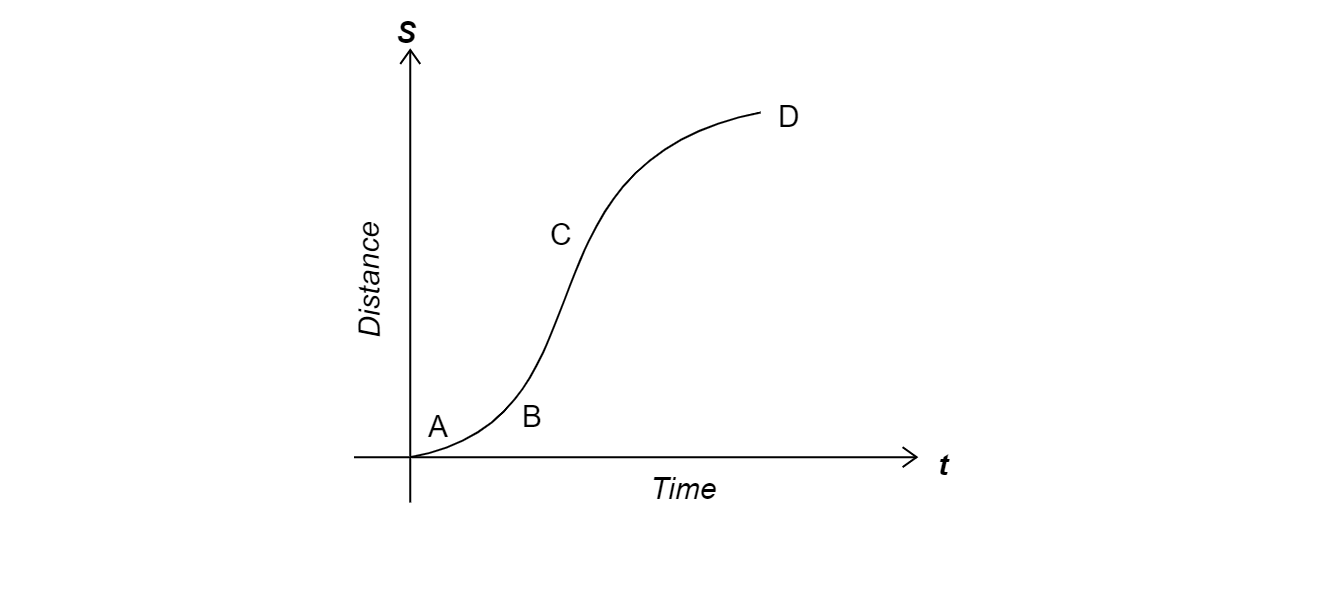
A particle shows a distance-time curve as given in this figure. The maximum instantaneous velocity of the particle will be noticed around which point?

Answer 1

Hint: First, we have to know how to understand a distance-time graph. Then we will try to understand how we can find out the instantaneous velocity just by looking at a distance-time graph. After that, we will compare the instantaneous velocities of the given points.

Complete solution:
In a distance-time graph, there are two axes. In our everyday use of such a graph, we make X-axis as the time axis and Y-axis as the distance axis. Here the distance $s$ is given as a function of time $t$.
Hence we can say, $s = f(t)$
If we differentiate $s$ with respect to $t$, we will get $f'(t)$ , giving us the instantaneous velocity at any point. This means-
$f'(t) = \dfrac{{ds}}{{dt}} = $ Instantaneous velocity $ = $ Slope of the curve at the concerning point
Therefore instantaneous velocity will be maximum where the slope of the curve is maximum.
If we look at the given figure, it is clear that at the point ${\text{B}}$ and ${\text{C}}$ the curve's slope is greater than at point ${\text{A}}$ and ${\text{D}}$. Then we look at points ${\text{B}}$ and ${\text{C}}$ , and it clarifies that point ${\text{C}}$ has a larger slope than the point${\text{B}}$.
Hence the particle has the maximum instantaneous velocity around the point ${\text{C}}$ as the Distance-Time graph has a larger slope around the point ${\text{C}}$.

Note: Similarly, we can find the acceleration of the particle around any point. For this, we have to double differentiate the displacement, which will be a function of time. However, always remember one can not determine if the acceleration will be maximum or minimum around a point just by looking at the distance-time graph.