Question

A particle rests on the top of a hemisphere of radius $R$. The minimum linear horizontal velocity for the particle to leave the vertex without slipping will be
A. $v = \sqrt {2gR} $
B. $v = \sqrt {\dfrac{{Rg}}{2}} $
C. $v = \sqrt {gR} $
D. $v = \sqrt {\dfrac{{2g}}{R}} $

Answer 1

Hint:Assuming a particle at rest on the top of a hemisphere whose radius is R given in the question. Using the problem statement equating the grapiticanal force and force due to the velocity or we can say outward force so that the particle leaves the vertex without sipping.

Complete step by step answer:

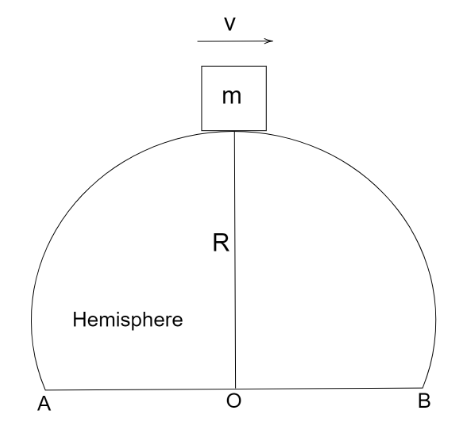
As per the problem a particle rests on the top of a hemisphere of radius R. We need to find the velocity for the particle to leave the vertex without slipping. From the above statement we conclude that the force due to gravity will be equal to force due to the velocity or we can say outward force on the particle so that particle leaves the vertex without slipping or in other words we can say that external forces acting on the particle is zero.

With help of this above discussion we can write,
Force due to gravity = force due to the velocity or outward force
Mathematically we can write,
$mg = \dfrac{{m{v^2}}}{R}$
Where, Mass of the particle= m
Acceleration due to gravity= g
Radius of the hemisphere= R
Velocity of the particle= v

Now,
$mg = \dfrac{{m{v^2}}}{R}$
Canceling the common terms we get,
$g = \dfrac{{{v^2}}}{R}$
Rearranging the above equation we get,
$ \Rightarrow {v^2} = gR$
$ \therefore v = \sqrt {gR} $

Therefore the correct option is $\left( C \right)$.

Note:In these types of problems we need to make all the external force to zero so as to avoid any kind of slipping in the body. Also it is very important to know that that outward force we are taking is known as centrifugal force acting on the particle. Here normal force is considered to be zero as it leaves the surface.