Question

A particle of mass m is kept on a fixed, smooth sphere of radius R at a position where the radius through the particle makes an angle of 30$^\circ $ with the vertical. The particle is released from this position.
(a) What is the force exerted by the sphere just after the release?
(b) Find the distance travelled by the particle before it leaves contact with the sphere.

Answer 1

Hint: First we need to draw a free body diagram showing all the forces acting on the particle. Then by studying the obtained equations involving the normal reaction force and the change in angle, we obtain the answer for two parts.

Complete answer:

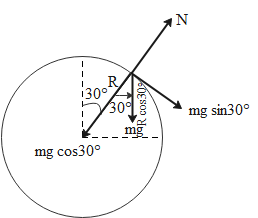
The figure shows a free body diagram which shows the given particle and the various forces acting on it.
(a) When this particle is released then the sphere will exert a normal reaction force on the particle which will equal the component of the weight of the particle acting opposite to the direction of the normal reaction force. From the diagram, we have
$N = mg\cos 30^\circ = \dfrac{{\sqrt 3 mg}}{2}$
This is the magnitude of the force which will be exerted by the sphere just after the release of the particle.

(b) The point at which the particle will leave the surface, the normal reaction force will be zero there. Let the angle of the radius at that point with vertical be $\theta $. If v is the velocity of that particle at this point then we can write the following expression, then at this point the force due to weight of the particle will create a centripetal force which will make the particle move on the spherical surface. Therefore, we have
$
  \dfrac{{m{v^2}}}{R} = mg\cos \theta \\
   \Rightarrow {v^2} = gR\cos \theta \\
 $
Now we can apply the work energy theorem to the system in the following way.
$W = {K_f} - {K_i}$
$
  mgh = \dfrac{1}{2}m{v^2} - 0 \\
\Rightarrow mgR\left( {\cos 30^\circ - \cos \theta } \right) = \dfrac{1}{2}mgR\cos \theta \\
\Rightarrow \dfrac{{\sqrt 3 }}{2} - \cos \theta = \dfrac{1}{2}\cos \theta \\
\Rightarrow \dfrac{3}{2}\cos \theta = \dfrac{{\sqrt 3 }}{2} \\
\Rightarrow \cos \theta = \dfrac{1}{{\sqrt 3 }} \\
\therefore \theta = {\cos ^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right) \\
 $
The actual distance that will be covered by the particle will be the circular arc from the angle of $30^\circ $ to $\theta $. Therefore angular displacement can be written as $\Delta \theta = \theta - \dfrac{\pi }{6}$. The path covered is given as $R\Delta \theta = R\left( {\theta - \dfrac{\pi }{6}} \right) = R\left\{ {{{\cos }^{ - 1}}\left( {\dfrac{1}{{\sqrt 3 }}} \right) - \dfrac{\pi }{6}} \right\}$.
This is the required answer.

Note:
According to the work energy theorem, the work done by the particle will equal to the change in the kinetic energy of the particle. Initially the particle is at rest with zero kinetic energy then it acquires a velocity v and the work done is due to the change in position of the particle from $R\cos 30^\circ $ to $R\cos \theta $.