Question

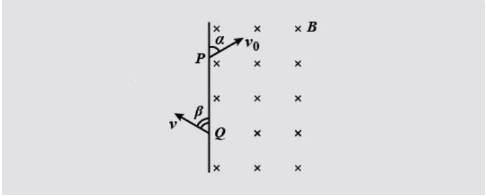
A particle of charge $ - q$ and mass $m$ enters a uniform magnetic field $B$ (perpendicular to paper inward) at $P$ with a velocity ${v_0}$ at an angle $\alpha $ and leaves the field at $Q$ with velocity $v$ at angle $\beta $ as shown in the figure:
 

This question has multiple correct options.
A) $\alpha = \beta $
B) $v = {v_0}$
C) $PQ = \dfrac{{2m{v_0}\sin \alpha }}{{Bq}}$
D) The particle remains in field for time $t = \dfrac{{2m\left( {\pi - \alpha } \right)}}{{Bq}}$

Answer 1

Hint: The charge will follow the path of the circle inside the magnetic field. So we can find distance between entering point and returning point using some geometry of the circle in which the charged particle will move and length of trajectory inside the magnetic field to, that will be a sector of the circle to determine time taken to cover this path.

Complete solution:
We know that the magnetic field is uniform and the magnetic field does not decrease the energy of a particle. Hence, the initial velocity of the particle will be equal to the final velocity of the particle.
Therefore, option (B) is correct.
Since, the magnetic field is perpendicular to the direction of initial velocity of charged particle, so a force , perpendicular to direction of particle velocity, will be acting over the particle continuously, while the particle will be inside the magnetic field.
This states the particle trajectory will be circle inside magnetic field, therefore, due to symmetry, $\alpha = \beta $
Hence, option (A) is correct.
The force \[F\] acting on the particle is denoted by,
$F = q\left( {v \times B} \right)$
Where $q$ is the charge of particle,
$v$ is velocity of particle,
$B$ is magnetic field
$ \times $ denotes cross product here.
Since, the velocity and magnetic field are perpendicular here,
So, $F = qvB\sin 90^\circ $
Which denotes, $F = qvB$
Let the radius of the circle be $r$
Since, the particle is moving in circle, a centripetal force will be acting on circle denoted by,
${F_c} = \dfrac{{m{v^2}}}{r}$
Where m is mass of particle,
This centripetal force is equal to magnetic force, so
$\dfrac{{m{v^2}}}{r} = qvB$
So we get,
$r = \dfrac{{mv}}{{qB}}$
Now, distance $PQ = 2r\sin \alpha $ (according to geometry of circle)
Putting value of radius in above equation,
$PQ = 2\dfrac{{mv}}{{qB}}\sin \alpha $
Hence, option (C) is correct.
Now, length of path will be \[\left( {2\pi - 2\alpha } \right)r\]
There fore time taken to cover this path will be,
$t = \dfrac{{\left( {2\pi - 2\alpha } \right)r}}{v}$
Purring value of radius in above equation,
$t = \dfrac{{\left( {2\pi - 2\alpha } \right)}}{v}\dfrac{{mv}}{{qB}}$
On solving we get,
$t = \dfrac{{2m\left( {\pi - \alpha } \right)}}{{qB}}$
Hence, option (D) is correct.

Hence, correct answers are options (A), (B), (C) and (D).

Note: The trajectory of particle was circle in the region of magnetic field only because direction of magnetic field was perpendicular to particle’s velocity otherwise, magnetic force would make the particle to move in a helix with one extra velocity in the direction which is perpendicular to both velocity and magnetic field.