Question

A particle moves over three quarters of a circle of radius $r$ . What is the magnitude of its displacement?

Answer 1

Hint: In order to solve this question we need to understand distance and displacement. Distance is defined as total path length travelled by particle from one point to another point, it is scalar quantity, while displacement is defined as the shortest distance between initial and final point, it does not depends on the path travelled rather it only depends on the initial and final points. Also displacement is a vector quantity because it has both magnitude and direction, also two displacements can be added by triangle rule of vector addition.

Complete step by step answer:
Consider a circle of radius r having center at O. Let the particle start from point A and start moving along the circumference, as he moves he starts to cover some distance, suppose after covering three- fourth of circumference it stops, so initial position of a particle is A and final position of the particle is B. So the displacement is defined as the shortest distance between initial point A and final point B.

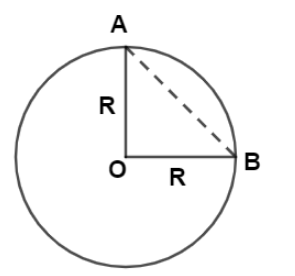
So we draw a straight line connecting both points, so the displacement magnitude is the length of AB that is, $d = AB$. Using Pythagoras law in $\Delta AOB$ we get,
$A{O^2} + B{O^2} = A{B^2}$
Since, $AO\& BO$ both are radius of circle so, $AO = BO = R$
Putting values of AO and BO we get, ${R^2} + {R^2} = A{B^2}$
$A{B^2} = 2{R^2}$
$\therefore AB = \sqrt 2 R$

So displacement is equal to, $AB = d = \sqrt 2 R$.

Note: It should be remembered that displacement is always the distance between the initial point and final point and displacement may be equal or less than the distance covered by the body but never greater than the distance covered by the body. and in this problem the distance covered by the body is the length of the three fourth part of the circle which is $\dfrac{{3\pi R}}{2}$.